
【題目】平面直角坐標(biāo)系![]() 中,已知直線
中,已知直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (s為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),以x軸正半軸為極軸建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為
(s為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),以x軸正半軸為極軸建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為![]() ,
,![]() ,直線與曲線C交于A,B兩點(diǎn).
,直線與曲線C交于A,B兩點(diǎn).
(Ⅰ)求直線l的普通方程和曲線C的直角坐標(biāo)方程;
(Ⅱ)已知點(diǎn)P的極坐標(biāo)為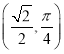 ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)![]() 的普通方程為:
的普通方程為:![]() ;曲線C的直角坐標(biāo)方程為
;曲線C的直角坐標(biāo)方程為![]() . (Ⅱ)
. (Ⅱ)![]()
【解析】
(Ⅰ)由直線![]() 的參數(shù)方程能求出
的參數(shù)方程能求出![]() 的普通方程,由曲線
的普通方程,由曲線![]() 的極坐標(biāo)方程轉(zhuǎn)為
的極坐標(biāo)方程轉(zhuǎn)為![]() ,能求出曲線
,能求出曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)![]() 的角坐標(biāo)為
的角坐標(biāo)為![]() ,直線
,直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),代入曲線
為參數(shù)),代入曲線![]() 的直角坐標(biāo)方程,結(jié)合韋達(dá)定理可得結(jié)果.
的直角坐標(biāo)方程,結(jié)合韋達(dá)定理可得結(jié)果.
(Ⅰ)∵直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),
為參數(shù)),
∴![]() 的普通方程為:
的普通方程為:![]() ;
;
又∵曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,即
,即![]() ,
,
∴曲線![]() 的直角坐標(biāo)方程為
的直角坐標(biāo)方程為![]() ,
,
即曲線![]() 的直角坐標(biāo)方程為:
的直角坐標(biāo)方程為:![]() .
.
(Ⅱ)點(diǎn)P的極坐標(biāo)為 ,其直角坐標(biāo)為
,其直角坐標(biāo)為![]() ,
,
直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù))
為參數(shù))
代入曲線![]() 的直角坐標(biāo)方程得
的直角坐標(biāo)方程得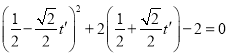 ,
,
即![]() ,
,
∴![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() 中,角
中,角![]() ,
,![]() ,
,![]() 的對(duì)邊分別為
的對(duì)邊分別為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,________.是否存在以
,________.是否存在以![]() ,
,![]() ,
,![]() 為邊的三角形?如果存在,求出
為邊的三角形?如果存在,求出![]() 的面積;若不存在,說(shuō)明理由.
的面積;若不存在,說(shuō)明理由.
從①![]() ;②
;②![]() ;③
;③![]() 這三個(gè)條件中任選一個(gè),補(bǔ)充在上面問(wèn)題中并作答.
這三個(gè)條件中任選一個(gè),補(bǔ)充在上面問(wèn)題中并作答.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() (
(![]() ).
).
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)![]() 時(shí),對(duì)任意的
時(shí),對(duì)任意的![]() ,
,![]() ,且
,且![]() ,都有
,都有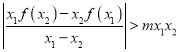 ,求實(shí)數(shù)m的取值范圍.
,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() .
.
(Ⅰ)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若![]() ,討論關(guān)于x的方程
,討論關(guān)于x的方程![]() 在區(qū)間
在區(qū)間![]() 上實(shí)根的個(gè)數(shù).
上實(shí)根的個(gè)數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)F為橢圓![]() 的右焦點(diǎn),點(diǎn)A為橢圓的右頂點(diǎn).
的右焦點(diǎn),點(diǎn)A為橢圓的右頂點(diǎn).
(1)求過(guò)點(diǎn)F、A且和直線![]() 相切的圓C的方程;
相切的圓C的方程;
(2)過(guò)點(diǎn)F任作一條不與![]() 軸重合的直線
軸重合的直線![]() ,直線
,直線![]() 與橢圓交于P,Q兩點(diǎn),直線PA,QA分別與直線
與橢圓交于P,Q兩點(diǎn),直線PA,QA分別與直線![]() 相交于點(diǎn)M,N.試證明:以線段MN為直徑的圓恒過(guò)點(diǎn)F.
相交于點(diǎn)M,N.試證明:以線段MN為直徑的圓恒過(guò)點(diǎn)F.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】程大位是明代著名數(shù)學(xué)家,他的《新編直指算法統(tǒng)宗》是中國(guó)歷史上一部影響巨大的著作.卷八中第33問(wèn):“今有三角果一垛,底闊每面七個(gè).問(wèn)該若干?”如圖是解決該問(wèn)題的程序框圖.執(zhí)行該程序框圖,求得該垛果子的總數(shù)S為( )

A.28B.56C.84D.120
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在兩個(gè)不同零點(diǎn),求實(shí)數(shù)
上存在兩個(gè)不同零點(diǎn),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】武漢出現(xiàn)的新型冠狀病毒是一種可以通過(guò)飛沫傳播的變異病毒,某藥物研究所為篩查該新型冠狀病毒,需要檢驗(yàn)血液是否為陽(yáng)性,現(xiàn)有![]() 份血液樣本,每份樣本取到的可能性均等,有以下兩種檢驗(yàn)方式:①逐份檢驗(yàn),則需要檢驗(yàn)n次;②混合檢驗(yàn),將其中
份血液樣本,每份樣本取到的可能性均等,有以下兩種檢驗(yàn)方式:①逐份檢驗(yàn),則需要檢驗(yàn)n次;②混合檢驗(yàn),將其中![]() 份血液樣本分別取樣混合在一起檢驗(yàn).若檢驗(yàn)結(jié)果為陰性,這k份血液全為陰性,因此這k份血液樣本檢驗(yàn)一次就夠了,如果檢驗(yàn)結(jié)果為陽(yáng)性,為了明確這k份血液究竟哪幾份為陽(yáng)性,就要對(duì)這k份血液再逐份檢驗(yàn),此時(shí)這k份血液的檢驗(yàn)次數(shù)總共為
份血液樣本分別取樣混合在一起檢驗(yàn).若檢驗(yàn)結(jié)果為陰性,這k份血液全為陰性,因此這k份血液樣本檢驗(yàn)一次就夠了,如果檢驗(yàn)結(jié)果為陽(yáng)性,為了明確這k份血液究竟哪幾份為陽(yáng)性,就要對(duì)這k份血液再逐份檢驗(yàn),此時(shí)這k份血液的檢驗(yàn)次數(shù)總共為![]() 次.假設(shè)在接受檢驗(yàn)的血液樣本中,每份樣本的檢驗(yàn)結(jié)果是陰性還是陽(yáng)性都是獨(dú)立的,且每份樣本是陽(yáng)性結(jié)果的概率為
次.假設(shè)在接受檢驗(yàn)的血液樣本中,每份樣本的檢驗(yàn)結(jié)果是陰性還是陽(yáng)性都是獨(dú)立的,且每份樣本是陽(yáng)性結(jié)果的概率為![]() .
.
(1)假設(shè)有5份血液樣本,其中只有2份為陽(yáng)性,若采取逐份檢驗(yàn)方式,求恰好經(jīng)過(guò)2次檢驗(yàn)就能把陽(yáng)性樣本全部檢驗(yàn)出來(lái)的概率;
(2)現(xiàn)取其中![]() 份血液樣本,記采用逐份檢驗(yàn)方式,樣本需要檢驗(yàn)的次數(shù)為
份血液樣本,記采用逐份檢驗(yàn)方式,樣本需要檢驗(yàn)的次數(shù)為![]() ,采用混合檢驗(yàn)方式,樣本需要檢驗(yàn)的總次數(shù)為
,采用混合檢驗(yàn)方式,樣本需要檢驗(yàn)的總次數(shù)為![]() .
.
(i)試運(yùn)用概率統(tǒng)計(jì)知識(shí),若![]() ,試求P關(guān)于k的函數(shù)關(guān)系式
,試求P關(guān)于k的函數(shù)關(guān)系式![]() ;
;
(ii)若![]() ,采用混合檢驗(yàn)方式可以使得這k份血液樣本需要檢驗(yàn)的總次數(shù)的期望值比逐份檢驗(yàn)的總次數(shù)期望值更少,求k的最大值.
,采用混合檢驗(yàn)方式可以使得這k份血液樣本需要檢驗(yàn)的總次數(shù)的期望值比逐份檢驗(yàn)的總次數(shù)期望值更少,求k的最大值.
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示的幾何體![]() 中,四邊形
中,四邊形![]() 是正方形,四邊形
是正方形,四邊形![]() 是梯形,
是梯形,![]()
![]()
![]() ,且
,且![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
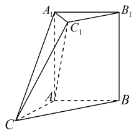
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,二面角
,二面角![]() 為
為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com