
���}Ŀ����֪�A ![]() �ķ��̞�
�ķ��̞� ![]() ��ֱ��
��ֱ�� ![]() �ķ��̞�
�ķ��̞� ![]() ���c(di��n)
���c(di��n) ![]() ��ֱ��
��ֱ�� ![]() �ϣ��^�c(di��n)
�ϣ��^�c(di��n) ![]() ���A
���A ![]() ���о�
���о� ![]() �����c(di��n)��
�����c(di��n)�� ![]() .
.
��1�����c(di��n) ![]() ������(bi��o)��
������(bi��o)�� ![]() �����о�
�����о� ![]() �ķ��̣�
�ķ��̣�
��2������߅�� ![]() ��e����Сֵ��
��e����Сֵ��
��3�����C����(j��ng)�^ ![]() ���c(di��n)�ĈA���^���c(di��n)����������ж��c(di��n)����(bi��o).
���c(di��n)�ĈA���^���c(di��n)����������ж��c(di��n)����(bi��o).
���𰸡�
��1���⣺�ٮ�(d��ng)�о�б�ʲ����ڕr(sh��)���о����̞� ![]() ��
��
�ڮ�(d��ng)�о�б�ʴ��ڕr(sh��)���O(sh��)�о����̞� ![]() ��
��
��?y��n)�ֱ���͈A���У����ԈA�� ![]() ���о��ľ��x
���о��ľ��x ![]() �����
����� ![]() ��
��
�����о����̞� ![]() ����
���� ![]() .
.
�ʴ𰸞飺�����о����̞� ![]() ��
�� ![]()
��2���⣺��߅�� ![]() ����e
����e ![]() ��
��
���Ԯ�(d��ng) ![]() ��С�r(sh��)����߅��
��С�r(sh��)����߅�� ![]() ����e
����e ![]() ��С.
��С.
�� ![]() ����Сֵ�LjA��
����Сֵ�LjA�� ![]() ��ֱ��
��ֱ�� ![]() �ľ��x��
�ľ��x��
�� ![]() .
.
�ʴ𰸞飺��߅�� ![]() ����e��Сֵ��
����e��Сֵ�� ![]() .
.
��3���C�����^ ![]() ���c(di��n)�ĈA����
���c(di��n)�ĈA���� ![]() ��ֱ���ĈA��
��ֱ���ĈA��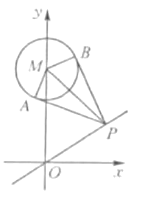
�O(sh��)�c(di��n) ![]() ���t�A������(bi��o)��
���t�A������(bi��o)�� ![]() ��
��
�� ![]() ��ֱ���ĈA�ķ�����
��ֱ���ĈA�ķ����� ![]()
![]() ��
��
����(ji��n)���� ![]() ��
��
�� ![]() .��*��
.��*��
�� ![]() �����
����� ![]() ��
�� 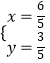 .
.
���ڲ�Փ ![]() ���ֵ���c(di��n)
���ֵ���c(di��n) ![]() ��
�� ![]() ������(bi��o)���m�Ϸ��̣�*�������Խ�(j��ng)�^
������(bi��o)���m�Ϸ��̣�*�������Խ�(j��ng)�^ ![]() ���c(di��n)�ĈA���^���c(di��n).
���c(di��n)�ĈA���^���c(di��n).
�ʴ𰸞飺���c(di��n)����(bi��o)�� ![]() ��
�� ![]() .
.
����������1�����ÈA�ĵ�ֱ���ľ��x������о����̣�ע��ֱ�����ڵ���r��
��2���Ȍ���߅�ε���e��ʾ��|PM|�ĺ���(sh��)ʽ��ͨ�^��|PM|����ֵ�õ���߅����e����ֵ��
��3�����A�ķ��̱�ʾ��Aϵ���̵���ʽ������A�^���c(di��n)������(bi��o).
�����c(di��n)�����������}���P(gu��n)�I���������c(di��n)��ֱ���ľ��x��ʽ�����P(gu��n)֪�R(sh��)�������c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x�飺
�ľ��x�飺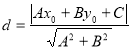 ��
��


 �����}���쾚ϵ�д�
�����}���쾚ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪ ![]() ���O(sh��)���}
���O(sh��)���} ![]() ��ָ��(sh��)����(sh��)
��ָ��(sh��)����(sh��) ![]() ��
�� ![]() ��
�� ![]() �φ��{(di��o)�f��.���}
�φ��{(di��o)�f��.���} ![]() ������(sh��)
������(sh��) ![]() �Ķ��x��?y��n)?
�Ķ��x��?y��n)?![]() ������
������ ![]() ����٣���
����٣��� ![]() �����棬��
�����棬�� ![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪ ![]() .
.
����(du��)һ�� ![]() ���������(sh��)��(sh��)
���������(sh��)��(sh��) ![]() ��ȡֵ������
��ȡֵ������
�����C������(du��)һ�� ![]() ������
������ ![]() ������
������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
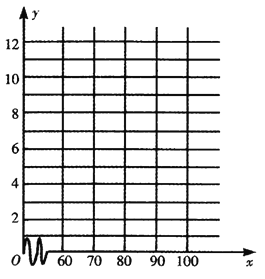
���}Ŀ��2015��һ�����y(t��ng)Ӌ(j��)��ij·���^��܇�v��܇�ٴ�С�c�l(f��)���Ľ�ͨ�¹ʴΔ�(sh��)���õ����±���ʾ�Ĕ�(sh��)��(j��)��

��1��Ո(q��ng)�����ϱ픵(sh��)��(j��)��ɢ�c(di��n)�D��
��2��Ո(q��ng)����(j��)�ϱ��ṩ�Ĕ�(sh��)��(j��)������С���˷����![]() �P(gu��n)��
�P(gu��n)��![]() �ľ��Իؚw����
�ľ��Իؚw����![]() ��
��
��3��ԇ����(j��)��2������ľ��Իؚw���̣��A(y��)�y(c��)��2016��ԓ·��·�r�����P(gu��n)��ȫ�O(sh��)ʩ�Ȳ�׃����r�£�܇���_(d��)��110![]() �r(sh��)�����ܰl(f��)���Ľ�ͨ�¹ʴΔ�(sh��).
�r(sh��)�����ܰl(f��)���Ľ�ͨ�¹ʴΔ�(sh��).
������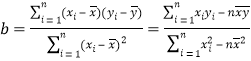 ��
��![]() ������
������![]() ��ӱ�ƽ��ֵ��
��ӱ�ƽ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����![]() ����
����![]() ����
����![]() ����(du��)��
����(du��)��![]() ����
����![]() ��B����
��B����![]() ����
����![]() �����xA�cB�IJ��
�����xA�cB�IJ��
![]() ��
��![]() ��A�cB֮�g�ľ��x��
��A�cB֮�g�ľ��x��![]() .
.
������![]() ����
����![]() ��
��
�����C������(du��)����![]() ����
����
��i��![]() ����
����![]() ��
��
��ii��![]() ����(g��)��(sh��)��������һ��(g��)��ż��(sh��)��
����(g��)��(sh��)��������һ��(g��)��ż��(sh��)��
����(du��)��![]() ��
��![]() ��
��![]() ���ٶ��xһ�NA�cB֮�g���\(y��n)�㣬�������ɗlԓ�\(y��n)��M������|(zh��)�������C����.
���ٶ��xһ�NA�cB֮�g���\(y��n)�㣬�������ɗlԓ�\(y��n)��M������|(zh��)�������C����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f��x��= ![]() sin��x��
sin��x�� ![]() cos��x���أ�0������y=f��x+
cos��x���أ�0������y=f��x+ ![]() ���ĈD���cy=f��x��
���ĈD���cy=f��x�� ![]() ���ĈD���غϣ�ӛ�ص����ֵ���0 �� ����(sh��)g��x��=cos����0x��
���ĈD���غϣ�ӛ�ص����ֵ���0 �� ����(sh��)g��x��=cos����0x�� ![]() ���Ć��{(di��o)�f���^(q��)�g�飨 ��
���Ć��{(di��o)�f���^(q��)�g�飨 ��
A.[�� ![]() ��+
��+ ![]() ����
���� ![]() +
+ ![]() ]��k��Z��
]��k��Z��
B.[�� ![]() +
+ ![]() ��
�� ![]() +
+ ![]() ]��k��Z��
]��k��Z��
C.[�� ![]() ��+2k����
��+2k���� ![]() +2k��]��k��Z��
+2k��]��k��Z��
D.[�� ![]() +2k����
+2k���� ![]() +2k��]��k��Z��
+2k��]��k��Z��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����(sh��)��![]() �У���(du��)����
����(du��)����![]() ����
����![]() ��
��![]() �鳣��(sh��)���������t�Q
�鳣��(sh��)���������t�Q![]() �顰�Ȳ�Ȕ�(sh��)�С������挦(du��)���Ȳ�Ȕ�(sh��)�С� ���Дࣺ��
�顰�Ȳ�Ȕ�(sh��)�С������挦(du��)���Ȳ�Ȕ�(sh��)�С� ���Дࣺ��![]() �����ܞ�
�����ܞ�![]() ���ڵȲ(sh��)��һ���ǵȲ�Ȕ�(sh��)�У� �۵ȱȔ�(sh��)��һ���ǵȲ�Ȕ�(sh��)�� ����ͨ�(xi��ng)��ʽ��
���ڵȲ(sh��)��һ���ǵȲ�Ȕ�(sh��)�У� �۵ȱȔ�(sh��)��һ���ǵȲ�Ȕ�(sh��)�� ����ͨ�(xi��ng)��ʽ��![]() ������
������![]() ����
����![]() ��
��![]() ���Ĕ�(sh��)��һ���ǵȲ�Ȕ�(sh��)�У��������_���Д��ǣ� ��
���Ĕ�(sh��)��һ���ǵȲ�Ȕ�(sh��)�У��������_���Д��ǣ� ��
A. �٢ۢ� B. �ڢۢ� C. �٢� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪?ji��ng)��c(di��n)P(x,y)(����y ![]() )��x�S�ľ��x�������c(di��n)F(0,1)�ľ��x��1.
)��x�S�ľ��x�������c(di��n)F(0,1)�ľ��x��1.
��1�����(d��ng)�c(di��n)P��܉�E���̣�
��2����ֱ��l��x-y+1=0�c��(d��ng)�c(di��n)P��܉�E����A��B���c(di��n)�����OAB����e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����и���(g��)�f(shu��)�����_���ǣ� ��
A. �K߅��ͬ�ĽǶ���� B. �g���ǵڶ����Ľ�
C. ��һ���Ľ����J�� D. �������Ľ���ؓ(f��)��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com