
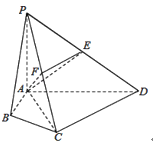
【題目】如圖,在長方體ABCD﹣HKLE中,底面ABCD是邊長為3的正方形,對角線AC與BD相交于點O,點F在線段AH上,且![]() ,BE與底面ABCD所成角為
,BE與底面ABCD所成角為![]() .
.
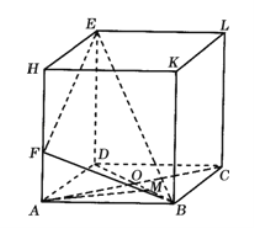
(1)求證:AC⊥BE;
(2)求二面角F﹣BE﹣D的余弦值;
(3)設(shè)點M在線段BD上,且AM//平面BEF,求DM的長.
【答案】(1)詳見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由題意可得DE⊥AC,AC⊥BD,根據(jù)線面垂直的判定可得AC⊥平面BDE,由線面垂直的性質(zhì)即可得證;
(2)由DA,DC,DE兩兩垂直,建立空間直角坐標系D﹣xyz,求出平面BEF的一個法向量![]() 、平面BDE的一個法向量
、平面BDE的一個法向量![]() ,由
,由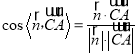 即可得解;
即可得解;
(3)設(shè)M(t,t,0),則![]() (t﹣3,t,0),由AM//平面BEF可得
(t﹣3,t,0),由AM//平面BEF可得![]() ,求得t后即可得解.
,求得t后即可得解.
(1)證明:因為在長方體ABCD﹣HKLE中, DE⊥平面ABCD,所以DE⊥AC,
因為四邊形ABCD是正方形,所以AC⊥BD,
又BD∩DE=D,所以AC⊥平面BDE,
而BE平面BDE,所以AC⊥BE;
(2)因為在長方體ABCD﹣HKLE中,DA,DC,DE兩兩垂直,
所以建立空間直角坐標系D﹣xyz如圖所示:
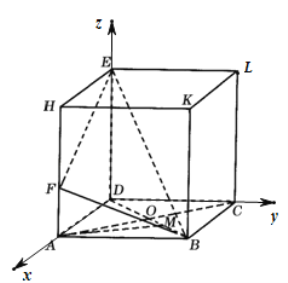
由DE⊥平面ABCD可知∠DBE為直線BE與平面ABCD所成的角,
又因為BE與平面ABCD所成角為![]() ,所以
,所以![]() ,
,
所以![]() ,由AD=3,可知
,由AD=3,可知![]() ,DE=
,DE=![]() ,
,
所以AH=3![]() ,
,
又2![]() 0,即AF
0,即AF![]() ,故AF
,故AF![]() ,
,
則A(3,0,0),F(3,0,![]() ),E(0,0,3
),E(0,0,3![]() ),B(3,3,0),C(0,3,0),
),B(3,3,0),C(0,3,0),
所以![]() (0,﹣3,
(0,﹣3,![]() ),
),![]() (3,0,﹣2
(3,0,﹣2![]() ),
),
設(shè)平面BEF的一個法向量為![]() (x,y,z),
(x,y,z),
則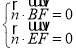 ,即
,即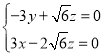 ,令
,令![]() ,則
,則![]() (4,2,
(4,2,![]() ),
),
因為AC⊥平面BDE,所以![]() 為平面BDE的一個法向量,
為平面BDE的一個法向量,![]() (3,﹣3,0),
(3,﹣3,0),
所以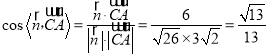 ,
,
因為二面角為銳角,所以二面角F﹣BE﹣D的余弦值為![]() ;
;
(3)因為點M是線段BD上一個動點,設(shè)M(t,t,0),則![]() (t﹣3,t,0),
(t﹣3,t,0),
因為AM//平面BEF,所以![]() ,
,
即4(t﹣3)+2t=0,解得t=2.
此時,點M坐標為(2,2,0),![]() ,符合題意.
,符合題意.


科目:高中數(shù)學(xué) 來源: 題型:
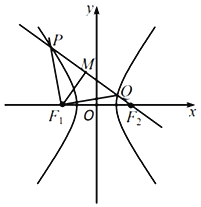
【題目】設(shè)雙曲線![]() 的左、右焦點分別為F1,F2,過點F2的直線分別交雙曲線左、右兩支于點P,Q,點M為線段PQ的中點,若P,Q,F1都在以M為圓心的圓上,且
的左、右焦點分別為F1,F2,過點F2的直線分別交雙曲線左、右兩支于點P,Q,點M為線段PQ的中點,若P,Q,F1都在以M為圓心的圓上,且![]() ,則雙曲線C的離心率為( )
,則雙曲線C的離心率為( )
A.![]() B.2
B.2![]() C.
C.![]() D.2
D.2![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
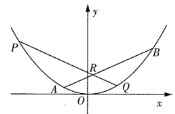
【題目】如圖,斜率為![]() 的直線交拋物線
的直線交拋物線![]() 于
于![]() 兩點,已知點
兩點,已知點![]() 的橫坐標比點
的橫坐標比點![]() 的橫坐標大4,直線
的橫坐標大4,直線![]() 交線段
交線段![]() 于點
于點![]() ,交拋物線于點
,交拋物線于點![]() .
.
(1)若點![]() 的橫坐標等于0,求
的橫坐標等于0,求![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《周髀算經(jīng)》有這樣一個問題:從冬至日起,依次小寒、大寒、立春、雨水、驚蟄、春分、清明、谷雨、立夏、小滿、芒種十二個節(jié)氣日影長減等寸,雨水、驚蟄、春分、清明日影之和為三丈二尺,前七個節(jié)氣日影之和為七丈三尺五寸,問谷雨日影長為( )
A.七尺五寸B.六尺五寸C.五尺五寸D.四尺五寸
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)![]() |2x﹣3|,g(x)
|2x﹣3|,g(x)![]() |2x+a+b|.
|2x+a+b|.
(1)解不等式f(x)![]() x2;
x2;
(2)當(dāng)a![]() 0,b
0,b![]() 0時,若F(x)
0時,若F(x)![]() f(x)+g(x)的值域為[5,+∞),求證:
f(x)+g(x)的值域為[5,+∞),求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 與直線
與直線![]() 只有一個公共點,點
只有一個公共點,點![]() 是拋物線
是拋物線![]() 上的動點.
上的動點.
(1)求拋物線![]() 的方程;
的方程;
(2)①若![]() ,求證:直線
,求證:直線![]() 過定點;
過定點;
②若![]() 是拋物線
是拋物線![]() 上與原點不重合的定點,且
上與原點不重合的定點,且![]() ,求證:直線
,求證:直線![]() 的斜率為定值,并求出該定值.
的斜率為定值,并求出該定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() 平面ABCD,E為PD的中點,
平面ABCD,E為PD的中點,![]() .
.
(1)求四棱錐![]() 的體積V;
的體積V;
(2)若F為PC的中點,求證:平面![]() 平面AEF;
平面AEF;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com