(本小題滿分12分)
已知直線
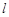
:
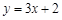
交拋物線
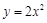
于
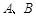
兩點,
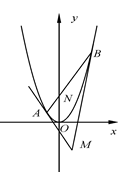
為坐標原點.
(Ⅰ)求
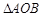
的面積;
(Ⅱ)設(shè)拋物線在點
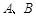
處的切線交于點
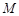
,求點
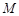
的坐標.
本試題主要是考查了只想愛你與拋物線的位置關(guān)系的綜合運用,以及三角形面積的最值的運用。
(1)由題意知直線
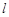
的斜率存在,設(shè)
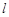
的方程為
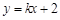
,然后與拋物線聯(lián)立方程組得到關(guān)于x的方程,結(jié)合韋達定理得到面積公式。
(2)根據(jù)
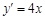
,
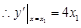
,得
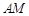
的方程為
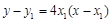
同理得到BM的方程,解得點M的坐標。
解:(Ⅰ)由題意得:
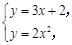
得
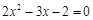
,∴
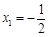
,
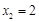
. 3分
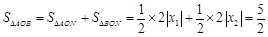
所以
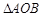
的面積為
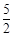
. 6分
(Ⅱ)由(Ⅰ)得:
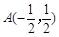
,
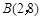
.
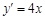
,
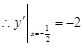
,
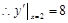
所以
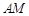
的方程為
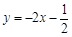
,
同理
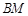
的方程為
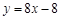
. 10分
兩方程聯(lián)立解得點
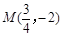
. 12分
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖6所示,等邊三角形OAB的邊長為8
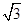
,且其三個頂點均在拋物線E:x2=2py(p>0)上.
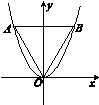
圖6
(1)求拋物線E的方程;
(2)設(shè)動直線l與拋物線E相切于點P,與直線y=-1相交于點Q,證明以PQ為直徑的圓恒過y軸上某定點.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
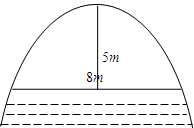
(本小題滿分10分)河上有一拋物線型拱橋,當水面距拱頂5
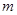
時,水面寬為8
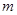
,一小船寬4
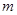
,高2
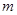
,載貨后船露出水面上的部分高
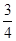
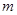
,問水面上漲到與拋物線拱頂相距多少米時,小船恰好能通行。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(13分)已知拋物線D的頂點是橢圓
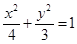
的中心,焦點與該橢圓的右焦點重合。
(1)求拋物線D的方程;
(2)已知動直線l過點P(4,0),交拋物線D于A,B兩點
(i)若直線l的斜率為1,求AB的長;
(ii)是否存在垂直于x軸的直線m被以AP為直徑的圓M所截得的弦長恒為定值?如果存在,求出m的方程,如果不存在,說明理由。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
.過拋物線
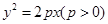
的焦點F作傾斜角為
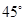
的直線交拋物線于A、B
兩點,若線段AB的長為8,則
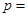
________________
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設(shè)
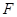
為拋物線
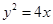
的焦點,直線
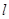
與其交于
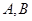
兩點,與
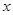
軸交于
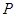
點,且以
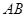
為直徑的圓過原點
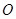
,則
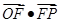
等于( )
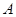
.
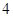
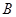
.
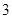
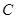
.
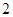
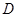
.
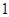
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
已知定點
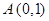
,直線
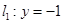
交
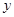
軸于點
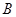
,記過點
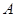
且與直線
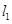
相切的圓的圓心為點
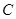
.
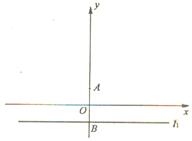
(I)求動點
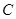
的軌跡
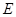
的方程;
(Ⅱ)設(shè)傾斜角為
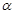
的直線
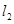
過點
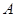
,交軌跡
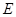
于兩點
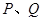
,交直線
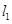
于點
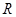
.若
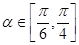
,求
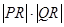
的最小值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
.設(shè)拋物線
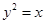
的焦點為F,點M在拋物線上,線段MF的延長線與直線
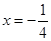
交于點N,則
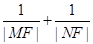
的值為
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
過拋物線
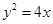
的焦點
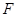
的直線交拋物線于
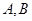
兩點,點
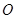
是原點,若
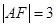
;則
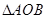
的面積為( )
查看答案和解析>>

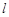 :
: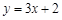 交拋物線
交拋物線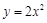 于
于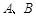 兩點,
兩點,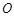 為坐標原點.
為坐標原點.
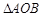 的面積;
的面積;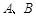 處的切線交于點
處的切線交于點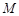 ,求點
,求點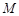 的坐標.
的坐標. 華東師大版一課一練系列答案
華東師大版一課一練系列答案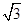 ,且其三個頂點均在拋物線E:x2=2py(p>0)上.
,且其三個頂點均在拋物線E:x2=2py(p>0)上.
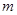 時,水面寬為8
時,水面寬為8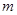 ,一小船寬4
,一小船寬4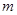 ,高2
,高2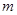 ,載貨后船露出水面上的部分高
,載貨后船露出水面上的部分高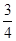
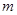 ,問水面上漲到與拋物線拱頂相距多少米時,小船恰好能通行。
,問水面上漲到與拋物線拱頂相距多少米時,小船恰好能通行。
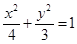 的中心,焦點與該橢圓的右焦點重合。
的中心,焦點與該橢圓的右焦點重合。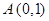 ,直線
,直線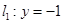 交
交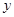 軸于點
軸于點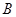 ,記過點
,記過點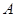 且與直線
且與直線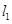 相切的圓的圓心為點
相切的圓的圓心為點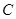 .
.
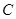 的軌跡
的軌跡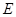 的方程;
的方程;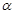 的直線
的直線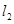 過點
過點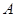 ,交軌跡
,交軌跡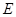 于兩點
于兩點 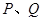 ,交直線
,交直線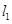 于點
于點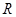 .若
.若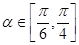 ,求
,求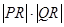 的最小值.
的最小值.