
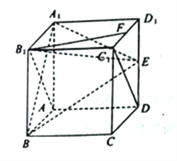
【題目】如圖,在長方體![]() 中,
中, ![]() 分別為
分別為![]() 的中點.
的中點.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)證明: ![]() 平面
平面![]() ;
;
(3)若正方體棱長為1,求四面體![]() 的體積.
的體積.
【答案】(1)詳見解析;(2) 詳見解析;(3) ![]() .
.
【解析】試題分析:(1)要證平面![]() 平面
平面![]() ,即證A1B⊥平面ADC1B1;(2)要證
,即證A1B⊥平面ADC1B1;(2)要證![]() 平面
平面![]() ,即證線線平行;(3)利用等積變換求四面體
,即證線線平行;(3)利用等積變換求四面體![]() 的體積.
的體積.
試題解析:
(1)如圖,因為ABCD-A1B1C1D1為正方體,所以B1C1⊥平面ABB1A1.
因為A1B![]() 平面ABB1A1,所以B1C1⊥A1B.
平面ABB1A1,所以B1C1⊥A1B.
因為A1B⊥AB1,B1C1∩AB1=B1,所以A1B⊥平面ADC1B1.
因為A1B![]() 平面A1BE,所以平面ADC1B1⊥平面A1BE
平面A1BE,所以平面ADC1B1⊥平面A1BE
(2)如圖,設AB1∩A1B=O,連接EF,OE.
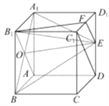
由已知條件得EF∥C1D,且EF= ![]() C1D.B1O∥C1D且B1O=
C1D.B1O∥C1D且B1O= ![]() C1D,
C1D,
所以EF∥B1O且EF=B1O,所以四邊形B1OEF為平行四邊形,
所以B1F∥OE,
因為B1F平面A1BE,OE![]() 平面A1BE,所以B1F∥平面A1BE
平面A1BE,所以B1F∥平面A1BE
(3) ![]() .
.


科目:高中數學 來源: 題型:
【題目】為了研究家用轎車在高速公路上的車速情況,交通部門隨機對50名家用轎車駕駛員進行調查,得到其在高速公路上行駛時的平均車速情況為:在30名男性駕駛員中,平均車速超過![]() 的有20人,不超過
的有20人,不超過![]() 的有10人.在20名女性駕駛員中,平均車速超過
的有10人.在20名女性駕駛員中,平均車速超過![]() 的有5人,不超過
的有5人,不超過![]() 的有15人.
的有15人.
(Ⅰ)完成下面的列聯表,并判斷是否有![]() 的把握認為平均車速超過
的把握認為平均車速超過![]() 的人與性別有關;
的人與性別有關;
平均車數超過
| 平均車速不超過
| 合計 | |
男性駕駛員人數 | |||
女性駕駛員人數 | |||
合計 |
(Ⅱ)以上述數據樣本來估計總體,現從高速公路上行駛的大量家用轎車中隨即抽取3輛,記這3輛車中駕駛員為女性且車速不超過![]() 的車輛數為
的車輛數為![]() ,若每次抽取的結果是相互獨立的,求
,若每次抽取的結果是相互獨立的,求![]() 的分布列和數學期望
的分布列和數學期望
參考公式:![]() ,其中
,其中![]() .
.
參考數據:
| 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC-A1B1C1中,△ABC是等邊三角形,BC=CC1=4,D是A1C1中點.
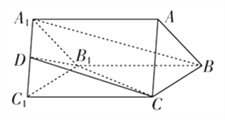
(1)求證:A1B∥平面B1CD;
(2)當三棱錐C-B1C1D體積最大時,求點B到平面B1CD的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)在R上是單調遞減的一次函數,且f(f(x))=4x-1.
(1)求f(x);
(2)求函數y=f(x)+x2-x在x∈[-1,2]上的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分) 某中學的環保社團參照國家環境標準制定了該校所在區域空氣質量指數與空氣質量等級對應關系如下表(假設該區域空氣質量指數不會超過![]() ):
):
空氣質量指數 |
|
|
|
|
|
|
空氣質量等級 |
|
|
|
|
|
|
該社團將該校區在![]() 年
年![]() 天的空氣質量指數監測數據作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.
天的空氣質量指數監測數據作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.
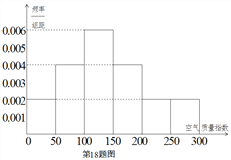
(Ⅰ)請估算![]() 年(以
年(以![]() 天計算)全年空氣質量優良的天數(未滿一天按一天計算);
天計算)全年空氣質量優良的天數(未滿一天按一天計算);
(Ⅱ)該校![]() 年
年![]() 月
月![]() 、
、![]() 日將作為高考考場,若這兩天中某天出現
日將作為高考考場,若這兩天中某天出現![]() 級重度污染,需要凈化空氣費用
級重度污染,需要凈化空氣費用![]() 元,出現
元,出現![]() 級嚴重污染,需要凈化空氣費用
級嚴重污染,需要凈化空氣費用![]() 元,記這兩天凈化空氣總費用為
元,記這兩天凈化空氣總費用為![]() 元,求
元,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
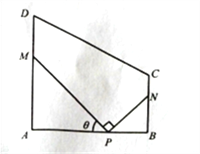
【題目】某地方政府要將一塊如圖所示的直角梯形ABCD空地改建為健身娛樂廣場.已知AD//BC, ![]() 百米,
百米, ![]() 百米,廣場入口P在AB上,且
百米,廣場入口P在AB上,且![]() ,根據規劃,過點P鋪設兩條相互垂直的筆直小路PM,PN(小路的寬度不計),點M,N分別在邊AD,BC上(包含端點),
,根據規劃,過點P鋪設兩條相互垂直的筆直小路PM,PN(小路的寬度不計),點M,N分別在邊AD,BC上(包含端點),![]() 區域擬建為跳舞健身廣場,
區域擬建為跳舞健身廣場, ![]() 區域擬建為兒童樂園,其它區域鋪設綠化草坪,設
區域擬建為兒童樂園,其它區域鋪設綠化草坪,設![]() .
.
(1)求綠化草坪面積的最大值;
(2)現擬將兩條小路PNM,PN進行不同風格的美化,PM小路的美化費用為每百米1萬元,PN小路的美化費用為每百米2萬元,試確定M,N的位置,使得小路PM,PN的美化總費用最低,并求出最小費用.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1: ![]() (t為參數)曲線C2:
(t為參數)曲線C2:![]() +y2=4.
+y2=4.
(1)在同一平面直角坐標系中,將曲線C2上的點按坐標變換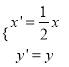 后得到曲線C′。求曲線C′的普通方程,并寫出它的參數方程;
后得到曲線C′。求曲線C′的普通方程,并寫出它的參數方程;
(2)若C1上的點P對應的參數為t=π/2,Q為C′上的動點,求PQ中點M到直線C3: ![]() (t為參數)的距離的最小值
(t為參數)的距離的最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(10分)設![]() 和
和![]() 分別是先后拋擲一枚骰子得到的點數,用隨機變量
分別是先后拋擲一枚骰子得到的點數,用隨機變量![]() 表示方程
表示方程
![]() 實根的個數(重根按一個計).
實根的個數(重根按一個計).
(Ⅰ)求方程![]() 有實根的概率;
有實根的概率;
(Ⅱ)求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅲ)求在先后兩次出現的點數中有5的條件下,方程![]() 有實根的概率.
有實根的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com