
【題目】已知函數![]() .
.
(Ⅰ)求函數y=f(x)圖象的對稱軸和對稱中心;
(Ⅱ)若函數![]() ,
,![]() 的零點為x1,x2,求cos(x1﹣x2)的值.
的零點為x1,x2,求cos(x1﹣x2)的值.
【答案】(Ⅰ)對稱軸方程為x![]() ,k∈Z,對稱中心為(
,k∈Z,對稱中心為(![]() ,0),k∈Z;(Ⅱ)±
,0),k∈Z;(Ⅱ)±![]() .
.
【解析】
(Ⅰ)先利用三角恒等變換化簡目標函數,然后求解對稱軸和對稱中心;
(Ⅱ)先求出![]() 的零點,然后求解cos(x1﹣x2)的值.
的零點,然后求解cos(x1﹣x2)的值.
函數![]() sin4x
sin4x![]() cos4x=sin(4x
cos4x=sin(4x![]() ),
),
(Ⅰ)由4x![]() ,k∈Z,可得f(x)的對稱軸方程為x
,k∈Z,可得f(x)的對稱軸方程為x![]() ,k∈Z,
,k∈Z,
令4x![]() kπ,k∈Z,則x
kπ,k∈Z,則x![]() ,k∈Z,∴f(x)的對稱中心為(
,k∈Z,∴f(x)的對稱中心為(![]() ,0),k∈Z;
,0),k∈Z;
(Ⅱ)根據函數![]() ,可得g(x)=sin(4x
,可得g(x)=sin(4x![]() )
)![]() ,
,![]() 的零點為x1,x2,
的零點為x1,x2,
∴sin(4x1![]() )
)![]() 0,即sin(4x1
0,即sin(4x1![]() )
)![]() ,∴2sin(2x1
,∴2sin(2x1![]() )cos(2x1
)cos(2x1![]() )
)![]() ,
,
∴![]() ,∴
,∴![]() .
.
由(Ⅰ)知,f(x)在![]() 內的對稱軸為x
內的對稱軸為x![]() ,則x1+x2
,則x1+x2![]() ,∴x2
,∴x2![]() x1,
x1,
∴cos(x1﹣x2)=cos(x1﹣(![]() x1)=cos(2x1
x1)=cos(2x1![]() )=sin(
)=sin(![]() 2x1
2x1![]() )
)
=sin(2x1![]() )=sin(2x1
)=sin(2x1![]() )
)
![]()
=±![]() .
.


 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,圓O的直徑AB=6,C為圓周上一點,BC=3,平面PAC垂直圓O所在平面,直線PC與圓O所在平面所成角為60°,PA⊥PC.
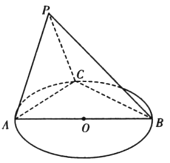
(1)證明:AP⊥平面PBC
(2)求二面角P—AB一C的余弦值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的長軸長為4,左、右頂點分別為
的長軸長為4,左、右頂點分別為![]() ,經過點
,經過點![]() 的動直線與橢圓
的動直線與橢圓![]() 相交于不同的兩點
相交于不同的兩點![]() (不與點
(不與點![]() 重合).
重合).
(1)求橢圓![]() 的方程及離心率;
的方程及離心率;
(2)求四邊形![]() 面積的最大值;
面積的最大值;
(3)若直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,判斷點
,判斷點![]() 是否位于一條定直線上?若是,寫出該直線的方程. (結論不要求證明)
是否位于一條定直線上?若是,寫出該直線的方程. (結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
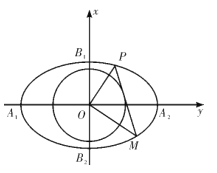
【題目】如圖,已知橢圓![]() 的左、右頂點為
的左、右頂點為![]() ,
,![]() ,上、下頂點為
,上、下頂點為![]() ,
,![]() ,記四邊形
,記四邊形![]() 的內切圓為
的內切圓為![]() .
.
(1)求圓![]() 的標準方程;
的標準方程;
(2)已知圓![]() 的一條不與坐標軸平行的切線
的一條不與坐標軸平行的切線![]() 交橢圓
交橢圓![]() 于P,M兩點.
于P,M兩點.
(i)求證:![]() ;
;
(ii)試探究![]() 是否為定值.
是否為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某種細菌的適宜生長溫度為10℃~25℃,為了研究該種細菌的繁殖數量![]() (單位:個)隨溫度
(單位:個)隨溫度![]() (單位:℃)變化的規律,收集數據如下:
(單位:℃)變化的規律,收集數據如下:
溫度 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
繁殖數量 | 20 | 25 | 33 | 27 | 51 | 112 | 194 |
對數據進行初步處理后,得到了一些統計量的值,如下表所示:
|
|
|
|
|
|
|
18 | 66 | 3.8 | 112 | 4.3 | 1428 | 20.5 |
其中![]() ,
,![]() .
.

(1)請繪出![]() 關于
關于![]() 的散點圖,并根據散點圖判斷
的散點圖,并根據散點圖判斷![]() 與
與![]() 哪一個更適合作為該種細菌的繁殖數量
哪一個更適合作為該種細菌的繁殖數量![]() 關于溫度
關于溫度![]() 的回歸方程類型(給出判斷即可,不必說明理由);
的回歸方程類型(給出判斷即可,不必說明理由);
(2)根據(1)的判斷結果及表格數據,建立![]() 關于
關于![]() 的回歸方程(結果精確到0.1);
的回歸方程(結果精確到0.1);
(3)當溫度為25℃時,該種細菌的繁殖數量的預報值為多少?
參考公式:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二成估計分別為
的斜率和截距的最小二成估計分別為 ,
,![]() .
.
參考數據:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國南宋數學家楊輝1261年所著的《詳解九章算法》一書里出現了如圖所示的表,即楊輝三角,這是數學史上的一個偉大成就,在“楊輝三角”中,第![]() 行的所有數字之和為
行的所有數字之和為![]() ,若去除所有為1的項,依次構成數列2,3,3,4,6,4,5,10,10,5,…,則此數列的前15項和為( )
,若去除所有為1的項,依次構成數列2,3,3,4,6,4,5,10,10,5,…,則此數列的前15項和為( )
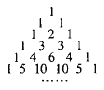
A. 110B. 114C. 124D. 125
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知圓![]() ,拋物線
,拋物線![]() 的頂點為
的頂點為![]() ,準線的方程為
,準線的方程為![]() ,
,![]() 為拋物線
為拋物線![]() 上的動點,過點
上的動點,過點![]() 作圓
作圓![]() 的兩條切線與
的兩條切線與![]() 軸交于
軸交于![]() .
.

(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)若![]() ,求△
,求△![]() 面積
面積![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C的頂點為坐標原點O,對稱軸為x軸,其準線過點![]() .
.
(1)求拋物線C的方程;
(2)過拋物線焦點F作直線l,使得拋物線C上恰有三個點到直線l的距離都為![]() ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com