
【題目】己知某區甲、乙、丙三所學校的教師志愿者人數分別為240,160,80.為助力疫情防控,現采用分層抽樣的方法,從這三所學校的教師志愿者中抽取6名教師,參與“抗擊疫情·你我同行”下卡口執勤值守專項行動.
(Ⅰ)求應從甲、乙、丙三所學校的教師志愿者中分別抽取的人數;
(Ⅱ)設抽出的6名教師志愿者分別記為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,現從中隨機抽取2名教師志愿者承擔測試體溫工作.
,現從中隨機抽取2名教師志愿者承擔測試體溫工作.
(i)試用所給字母列舉出所有可能的抽取結果;
(ii)設![]() 為事件“抽取的2名教師志愿者來自同一所學校”,求事件
為事件“抽取的2名教師志愿者來自同一所學校”,求事件![]() 發生的概率.
發生的概率.
【答案】(Ⅰ)3人,2人,1人;(Ⅱ)(i)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;(ⅱ)
;(ⅱ)![]()
【解析】
(Ⅰ)按照分層抽樣規則計算可得;
(Ⅱ)(i)將所有可能結果一一列舉,做到不重復不遺漏;
(ii)根據古典概型的概率公式計算可得;
解:(Ⅰ)由已知,甲、乙、丙三所學校的教師志愿者人數之比為3:2:1
由于采用分層抽樣的方法從中抽取6名教師,因此應從甲、乙、丙三所學校的教師志愿者中分別抽取3人,2人,1人.
(Ⅱ)(ⅰ)從抽出的 名教師中隨機抽取2名教師的所有可能結果為
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共15種.
,共15種.
(ⅱ)由(Ⅰ),不妨設抽出的6名教師中,來自甲學校的是![]() ,
,![]() ,
,![]() ,來自乙學校的是
,來自乙學校的是![]() ,
,![]() ,來自丙學校的是
,來自丙學校的是![]() ,則從抽出的6名教師中隨機抽取的2名教師來自同一學校的所有可能結果為
,則從抽出的6名教師中隨機抽取的2名教師來自同一學校的所有可能結果為![]() ,
,![]() ,
,![]() ,
,![]() ,共4種.
,共4種.
所以,事件![]() 發生的概率
發生的概率![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖是一個幾何體的平面展開圖,其中四邊形![]() 為正方形,
為正方形,![]() ,
,![]() ,
,![]() ,
,![]() 為全等的等邊三角形,
為全等的等邊三角形,![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點,在此幾何體中,下列結論中正確的個數有()
的中點,在此幾何體中,下列結論中正確的個數有()
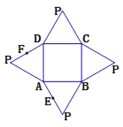
①平面![]() 平面
平面![]()
②直線![]() 與直線
與直線![]() 是異面直線
是異面直線
③直線![]() 與直線
與直線![]() 共面
共面
④面![]() 與面
與面![]() 的交線與
的交線與![]() 平行
平行
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學將100名高一新生分成水平相同的甲、乙兩個平行班,每班50人,某教師采用![]() 、
、![]() 兩種不同的教學模式分別在甲、乙兩個班進行教改實驗,為了了解教學效果,期末考試后,該教師分別從兩班中各隨機抽取20名學生的成績進行統計,作出莖葉圖如圖所示,記成績不低于90分為“成績優秀”.
兩種不同的教學模式分別在甲、乙兩個班進行教改實驗,為了了解教學效果,期末考試后,該教師分別從兩班中各隨機抽取20名學生的成績進行統計,作出莖葉圖如圖所示,記成績不低于90分為“成績優秀”.

(1)在乙班的20個個體中,從不低于86分的成績中隨機抽取2人,求抽出的兩個人均“成績優秀”的概率;
(2)由以上統計數據填寫![]() 列聯表;能否在犯錯誤的概率不超過0.10的前提下認為成績優秀與教學模型有關.
列聯表;能否在犯錯誤的概率不超過0.10的前提下認為成績優秀與教學模型有關.
甲班( | 乙班( | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.847 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著共享單車的成功運營,更多的共享產品逐步走人大家的世界,共享汽車、共享籃球、共享充電寶等各種共享產品層出不窮![]() 廣元某景點設有共享電動車租車點,共享電動車的收費標準是每小時2元
廣元某景點設有共享電動車租車點,共享電動車的收費標準是每小時2元![]() 不足1小時的部分按1小時計算
不足1小時的部分按1小時計算![]() 甲、乙兩人各租一輛電動車,若甲、乙不超過一小時還車的概率分別為
甲、乙兩人各租一輛電動車,若甲、乙不超過一小時還車的概率分別為![]() ;一小時以上且不超過兩小時還車的概率分別為
;一小時以上且不超過兩小時還車的概率分別為![]() ;兩人租車時間都不會超過三小時.
;兩人租車時間都不會超過三小時.
![]() Ⅰ
Ⅰ![]() 求甲、乙兩人所付租車費用相同的概率;
求甲、乙兩人所付租車費用相同的概率;
![]() Ⅱ
Ⅱ![]() 設甲、乙兩人所付的租車費用之和為隨機變量
設甲、乙兩人所付的租車費用之和為隨機變量![]() ,求
,求![]() 的分布列與數學期望
的分布列與數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D為線段AC的中點,E為線段PC上一點.
(1)求證:PA⊥BD;
(2)求證:平面BDE⊥平面PAC;
(3)當PA∥平面BDE時,求三棱錐E﹣BCD的體積.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場銷售某種商品的經驗表明,該商品每日的銷售量![]() (單位:千克)與銷售價格
(單位:千克)與銷售價格![]() (單位:元/千克)滿足關系式
(單位:元/千克)滿足關系式![]() ,其中
,其中![]() 為常數.已知銷售價格為5元/千克時,每日可售出該商品13千克.
為常數.已知銷售價格為5元/千克時,每日可售出該商品13千克.
(1)求![]() 的值;
的值;
(2)若該商品的成本為3元/千克,試確定銷售價格![]() 的值,使商場每日銷售該商品所獲得的利潤最大,并求出最大利潤.
的值,使商場每日銷售該商品所獲得的利潤最大,并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
![]() .
.
(1)當![]() 時,求
時,求![]() 的極值;
的極值;
(2)當![]() 時,若函數
時,若函數![]() 恰有兩個不同的零點,求
恰有兩個不同的零點,求![]() 的值;
的值;
(3)當![]() 時,若
時,若![]() 的解集為
的解集為![]() ,且
,且![]() 中有且僅有一個整數,求實數
中有且僅有一個整數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,四邊形
中,四邊形![]() 是邊長為2的正方形,
是邊長為2的正方形,![]() ,
,![]() 為
為![]() 的中點,點
的中點,點![]() 在
在![]() 上,
上,![]() 平面
平面![]() ,
,![]() 在
在![]() 的延長線上,且
的延長線上,且![]() .
.
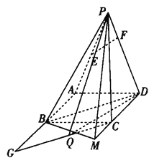
(1)證明:![]() 平面
平面![]() .
.
(2)過點![]() 作
作![]() 的平行線,與直線
的平行線,與直線![]() 相交于點
相交于點![]() ,點
,點![]() 為
為![]() 的中點,求
的中點,求![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com