【題目】等差數列的定義可用數學符號語言描述為________,其中
，其通項公式
_________,
__________=_________,等差數列中，若
則________(
)
智趣寒假作業云南科技出版社系列答案科目：高中數學 來源： 題型：
【題目】某少數民族的刺繡有著悠久的歷史，如圖4①，②，③，④為她們刺繡最簡單的四個圖案，這些圖案都是由小正方形構成，小正方形數越多刺繡越漂亮．現按同樣的規律刺繡(小正方形的擺放規律相同)，設第n個圖形包含f(n)個小正方形．
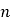
(1)求出f(5)的值；
(2)利用合情推理的“歸納推理思想”，歸納出f(n＋1)與f(n)之間的關系式，并根據你得到的關系式求出f(n)的表達式；
(3)求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知過拋物線
的焦點
的直線與拋物線交于
兩點，且
，拋物線的準線
與
軸交于
，
于點
，且四邊形
的面積為
，過
的直線
交拋物線于
兩點，且
，點
為線段
的垂直平分線與軸的交點，則點的橫坐標
的取值范圍為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，三棱柱
中，四邊形
為菱形，
，平面
平面
，
在線段
上移動，
為棱
的中點.
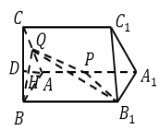
（1）若為線段的中點，
為
中點，延長
交
于
，求證：
平面
；
（2）若二面角
的平面角的余弦值為
，求點到平面
的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】橢圓
的左、右焦點為
，離心率為
，已知過
軸上一點
作一條直線
：
，交橢圓于
兩點，且
的周長最大值為8.
（1）求橢圓方程；
（2）以點
為圓心，半徑為
的圓的方程為
.過
的中點
作圓的切線
，
為切點，連接
，證明：當
取最大值時，點
在短軸上（不包括短軸端點及原點）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
圖象相鄰兩條對稱軸之間的距離為
，將函數
的圖象向左平移
個單位，得到的圖象關于
軸對稱，則（ ）
A. 函數
的周期為
B. 函數圖象關于點
對稱
C. 函數圖象關于直線
對稱 D. 函數在
上單調
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示的莖葉圖記錄了華潤萬家在渭南城區甲、乙連鎖店四天內銷售情況的某項指標統計：
（I）求甲、乙連鎖店這項指標的方差，并比較甲、乙該項指標的穩定性；
（Ⅱ）每次都從甲、乙兩店統計數據中隨機各選一個進行比對分析，共選了3次（有放回選取）．設選取的兩個數據中甲的數據大于乙的數據的次數為
，求的分布列及數學期望
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠生產某種型號的電視機零配件，為了預測今年
月份該型號電視機零配件的市場需求量，以合理安排生產，工廠對本年度
月份至
月份該型號電視機零配件的銷售量及銷售單價進行了調查，銷售單價
（單位：元）和銷售量
（單位：千件）之間的組數據如下表所示：
月份 |
|
|
|
|
|
|
銷售單價 |
|
|
|
|
|
|
銷售量 |
|
|
|
|
|
|
（1）根據1至月份的數據，求關于的線性回歸方程（系數精確到
）；
（2）結合（1）中的線性回歸方程，假設該型號電視機零配件的生產成本為每件
元，那么工廠如何制定月份的銷售單價，才能使該月利潤達到最大（計算結果精確到
）？
參考公式：回歸直線方程
，其中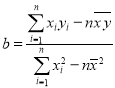
.
參考數據：
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
