
【題目】如圖所示的程序框圖的算法思路源于我國古代數學中的秦九韶算法,執行該程序框圖,則輸出的結果S表示的值為( ) 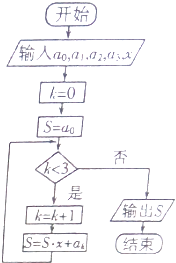
A.a0+a1+a2+a3
B.(a0+a1+a2+a3)x3
C.a0+a1x+a2x2+a3x3
D.a0x3+a1x2+a2x+a3
【答案】D
【解析】解:當k=0,S=a0時,滿足進行循環的條件,執行循環體后,k=1,S=a0x+a1 ,
當k=1,S=a0x+a1時,滿足進行循環的條件,執行循環體后,k=2,S=a0x2+a1x+a2 ,
當k=2,S=a0x2+a1x+a2時,滿足進行循環的條件,執行循環體后,k=3,S=a0x3+a1x2+a2x+a3 ,
當k=3,S=a0x3+a1x2+a2x+a3時,不滿足進行循環的條件,
故輸出結果為:a0x3+a1x2+a2x+a3 ,
故選:D
【考點精析】利用程序框圖對題目進行判斷即可得到答案,需要熟知程序框圖又稱流程圖,是一種用規定的圖形、指向線及文字說明來準確、直觀地表示算法的圖形;一個程序框圖包括以下幾部分:表示相應操作的程序框;帶箭頭的流程線;程序框外必要文字說明.


科目:高中數學 來源: 題型:
【題目】動點![]() 在拋物線
在拋物線![]() 上,過點
上,過點![]() 作
作![]() 垂直于
垂直于![]() 軸,垂足為
軸,垂足為![]() ,設
,設![]() .
.
(Ⅰ)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)若點![]() 是
是![]() 上的動點,過點
上的動點,過點![]() 作拋物線
作拋物線![]() :
:![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() ,設點
,設點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,求
,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩臺機床同時生產一種零件,10天中,兩臺機床每天出的次品數分別如下圖所示。
甲 | 0 | 1 | 0 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 2 | 3 | 1 | 1 | 0 | 2 | 1 | 1 | 0 | 1 |
從數據上看, ________________機床的性能較好(填“甲”或者“乙”).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設拋物線![]() 的準線
的準線![]() 與
與![]() 軸交于橢圓
軸交于橢圓![]() 的右焦點
的右焦點![]() 為
為![]() 的左焦點.橢圓的離心率為
的左焦點.橢圓的離心率為![]() ,拋物線
,拋物線![]() 與橢圓
與橢圓![]() 交于
交于![]() 軸上方一點
軸上方一點![]() ,連接
,連接![]() 并延長其交
并延長其交![]() 于點
于點![]() ,
, ![]() 為
為![]() 上一動點,且在
上一動點,且在![]() 之間移動.
之間移動.
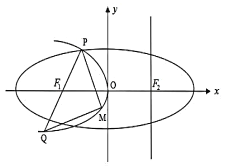
(1)當![]() 取最小值時,求
取最小值時,求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的邊長恰好是三個連續的自然數,當
的邊長恰好是三個連續的自然數,當![]() 面積取最大值時,求面積最大值以及此時直線
面積取最大值時,求面積最大值以及此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC= ![]() AB=
AB= ![]() ,平面PBC⊥平面ABCD.
,平面PBC⊥平面ABCD. 
(1)求證:AC⊥PB;
(2)若PB=PC= ![]() ,問在側棱PB上是否存在一點M,使得二面角M﹣AD﹣B的余弦值為
,問在側棱PB上是否存在一點M,使得二面角M﹣AD﹣B的余弦值為 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 C:![]() 的焦距為2,且過點
的焦距為2,且過點![]() ,右焦點為
,右焦點為![]() .設A,B 是C上的兩個動點,線段 AB 的中點M 的橫坐標為
.設A,B 是C上的兩個動點,線段 AB 的中點M 的橫坐標為![]() ,線段AB的中垂線交橢圓C于P,Q 兩點.
,線段AB的中垂線交橢圓C于P,Q 兩點.
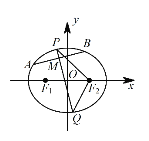
(1)求橢圓 C 的方程;
(2)設M點縱坐標為m,求直線PQ的方程,并求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知焦點在![]() 軸上的橢圓
軸上的橢圓![]() 過點
過點![]() ,且離心率為
,且離心率為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若直線![]() (
(![]() ,
,![]() )與橢圓C交于兩點A、B,點D滿足
)與橢圓C交于兩點A、B,點D滿足![]() ,經過點D及點
,經過點D及點![]() 的直線的斜率為
的直線的斜率為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 袋中有形狀、大小、質地完全一樣的![]() 個紅球和
個紅球和![]() 個白球,從中隨機抽出一個球,一定是紅球
個白球,從中隨機抽出一個球,一定是紅球
B. 天氣預報“明天降水概率![]() ”,是指明天有
”,是指明天有![]() 的時間會下雨
的時間會下雨
C. 某地發行一種福利彩票,中獎率是千分之一,那么,買這種彩票![]() 張,一定會中獎
張,一定會中獎
D. 連續擲一枚均勻硬幣,若![]() 次都是正面朝上,則第六次仍然可能正面朝上
次都是正面朝上,則第六次仍然可能正面朝上
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com