【題目】如圖所示，四棱錐
的底面為矩形，已知
， 
，過底面對角線
作與
平行的平面交
于
.
（1）試判定點
的位置，并加以證明；
（2）求二面角
的余弦值.
【答案】(1) 
為
的中點，見解析(2) 
【解析】試題分析：（1）由
平面
得到
，結合
為
的中點，即可得到答案；
（2）求出平面EAC的法向量和平面DAC的法向量，由此利用向量法能求出二面角
的平面角的余弦值．
試題解析：
（1）
為
的中點，證明如下：
連接
，因為
平面
，平面
平面
， 
平面
，所以
，又
為
的中點，所以
為
的中點.
（2）連接
，因為四邊形
為矩形，所以
.因為
，所以
.同理，得
，所以
平面
，以
為原點， 
為
軸，過
平行于
的直線為
軸，過
平行于
的直線為
軸建立空間直角坐標系（如圖所示）.
易知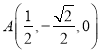
， 
， 
， 
， 
， 
，
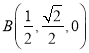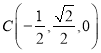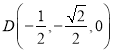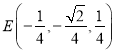則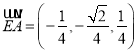
， 
.
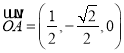顯然， 
是平面
的一個法向量.設
是平面
的一個法向量，
則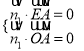
，即
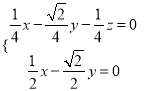，取
，
則
，
所以
，
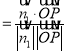
所以二面角
的余弦值為
.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓與拋物線y2＝
x有一個相同的焦點，且該橢圓的離心率為
.
(1)求橢圓的標準方程；
(2)過點P(0,1)的直線與該橢圓交于A，B兩點，O為坐標原點，若
，求△AOB的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】直線
ax＋by＝1與圓x2＋y2＝1相交于A，B兩點(其中a，b是實數)，且△AOB是直角三角形(O是坐標原點)，則點P(a，b)與點(0,1)之間距離的最小值為________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校從參加某次知識競賽測試的學生中隨機抽出60名學生，將其成績（百分制）（均為整數）分成六段
，
…
后得到如下部分頻率分布直方圖.觀察圖形的信息，回答下列問題：
（1）求分數在
內的頻率，并補全這個頻率分布直方圖；
（2）根據頻率分布直方圖，從圖中估計總體的眾數是多少分？中位數是多少分？
（3）統(tǒng)計方法中，同一組數據常用該組區(qū)間的中點值作為代表，據此估計本次考試的平均分.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知集合A＝{x|1<x<3}，集合B＝{x|2m<x<1－m}．
(1)當m＝－1時，求A∪B；
(2)若AB，求實數m的取值范圍；
(3)若A∩B＝，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某研究機構為了了解各年齡層對高考改革方案的關注程度，隨機選取了200名年齡在
內的市民進行了調查，并將結果繪制成如圖所示的頻率分布直方圖（分第一～五組區(qū)間分別為
，
，
，
，
，
）.
（1）求選取的市民年齡在內的人數；
（2）若從第3,4組用分層抽樣的方法選取5名市民進行座談，再從中選取2人在座談會中作重點發(fā)言，求作重點發(fā)言的市民中至少有一人的年齡在內的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著網絡的發(fā)展，網上購物越來越受到人們的喜愛，各大購物網站為增加收入，促銷策略越來越多樣化，促銷費用也不斷增加.下表是某購物網站2017年1-8月促銷費用（萬元）和產品銷量（萬件）的具體數據.
（1）根據數據繪制的散點圖能夠看出可用線性回歸模型擬合
與
的關系，請用相關系數
加以說明；（系數精確到0.001）
（2）建立
關于
的回歸方程
（系數精確到0.01）；如果該公司計劃在9月份實現產品銷量超6萬件，預測至少需投入促銷費用多少萬元（結果精確到0.01）.
參考數據： 
， 
， 
， 
， 
，其中
， 
分別為第
個月的促銷費用和產品銷量， 
.
參考公式：（1）樣本
的相關系數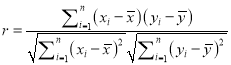
（2）對于一組數據
， 
， 
， 
，其回歸方程
的斜率和截距的最小二乘估計分別為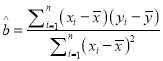
， 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f(x)是R上的奇函數，且當x>0時，f(x)＝－x2＋2x＋2.
(1)求f(x)的解析式；
(2)畫出f(x)的圖像，并指出f(x)的單調區(qū)間．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
