
傳說(shuō)古希臘畢達(dá)哥拉斯學(xué)派的數(shù)學(xué)家經(jīng)常在沙灘上畫點(diǎn)或用小石子表示數(shù). 他們研究過如圖所示的三角形數(shù):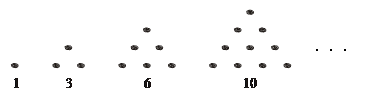
|
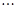 記為數(shù)列
記為數(shù)列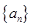 ,將可被5整除的三角形數(shù)按從小到大的順序組成一個(gè)新數(shù)列
,將可被5整除的三角形數(shù)按從小到大的順序組成一個(gè)新數(shù)列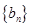 . 可以推測(cè):(Ⅰ)
. 可以推測(cè):(Ⅰ)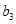 是數(shù)列
是數(shù)列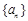 中的第 項(xiàng);
中的第 項(xiàng);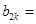 ________(用k表示)
________(用k表示) (Ⅰ)9;(Ⅱ)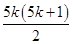
解析試題分析:(I)由題設(shè)條件可以歸納出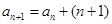 ,故
,故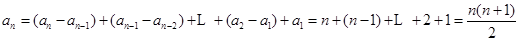 ,由此可知,第3個(gè)可被5整除的數(shù)為45,是數(shù)列
,由此可知,第3個(gè)可被5整除的數(shù)為45,是數(shù)列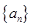 中的第9項(xiàng);
中的第9項(xiàng);
(II)由于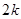 是偶數(shù),由(I)知,第
是偶數(shù),由(I)知,第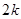 個(gè)被5整除的數(shù)出現(xiàn)在第
個(gè)被5整除的數(shù)出現(xiàn)在第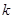 組倒數(shù)第一個(gè),故它是數(shù)列
組倒數(shù)第一個(gè),故它是數(shù)列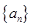 中的第
中的第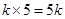 項(xiàng),所以
項(xiàng),所以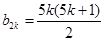 .
.
考點(diǎn):本小題主要考查數(shù)列的遞推關(guān)系,數(shù)列的表示及歸納推理,考查學(xué)生的歸納推理能力.
點(diǎn)評(píng):解決此小題的關(guān)鍵是由題設(shè)得出相鄰兩個(gè)三角形數(shù)的遞推關(guān)系,由此列舉出三角形數(shù).


 應(yīng)用題作業(yè)本系列答案
應(yīng)用題作業(yè)本系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
設(shè)a1,a2, ,an為正整數(shù),其中至少有五個(gè)不同值. 若對(duì)于任意的i,j(1≤i<j≤n),存在k,l(k≠l,且異于i與j)使得ai+aj=ak+al,則n的最小值是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
《萊因德紙草書》(Rhind Papyrus)是世界上最古老的數(shù)學(xué)著作之一。書中有一道這樣的題目:把100個(gè)面包分給五人,使每人成等差數(shù)列,且使最大的三份之和的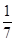 是較小的兩份之和,則最小1份的大小是
是較小的兩份之和,則最小1份的大小是
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本題滿分18分) 本題共有3個(gè)小題,第1小題滿分4分,第2小題滿分6分. 第3小題滿分8分.
(文)對(duì)于數(shù)列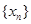 ,從中選取若干項(xiàng),不改變它們?cè)谠瓉?lái)數(shù)列中的先后次序,得到的數(shù)列稱為是原來(lái)數(shù)列的一個(gè)子數(shù)列. 某同學(xué)在學(xué)習(xí)了這一個(gè)概念之后,打算研究首項(xiàng)為
,從中選取若干項(xiàng),不改變它們?cè)谠瓉?lái)數(shù)列中的先后次序,得到的數(shù)列稱為是原來(lái)數(shù)列的一個(gè)子數(shù)列. 某同學(xué)在學(xué)習(xí)了這一個(gè)概念之后,打算研究首項(xiàng)為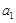 ,公差為
,公差為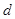 的無(wú)窮等差數(shù)列
的無(wú)窮等差數(shù)列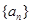 的子數(shù)列問題,為此,他取了其中第一項(xiàng)
的子數(shù)列問題,為此,他取了其中第一項(xiàng)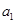 ,第三項(xiàng)
,第三項(xiàng)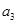 和第五項(xiàng)
和第五項(xiàng)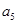 .
.
(1) 若 成等比數(shù)列,求
成等比數(shù)列,求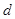 的值;
的值;
(2) 在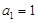 ,
, 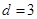 的無(wú)窮等差數(shù)列
的無(wú)窮等差數(shù)列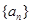 中,是否存在無(wú)窮子數(shù)列
中,是否存在無(wú)窮子數(shù)列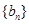 ,使得數(shù)列
,使得數(shù)列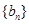 為等比數(shù)列?若存在,請(qǐng)給出數(shù)列
為等比數(shù)列?若存在,請(qǐng)給出數(shù)列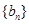 的通項(xiàng)公式并證明;若不存在,說(shuō)明理由;
的通項(xiàng)公式并證明;若不存在,說(shuō)明理由;
(3) 他在研究過程中猜想了一個(gè)命題:“對(duì)于首項(xiàng)為正整數(shù) ,公比為正整數(shù)
,公比為正整數(shù)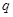 (
(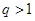 )的無(wú)窮等比數(shù) 列
)的無(wú)窮等比數(shù) 列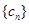 ,總可以找到一個(gè)子數(shù)列
,總可以找到一個(gè)子數(shù)列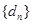 ,使得
,使得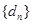 構(gòu)成等差數(shù)列”. 于是,他在數(shù)列
構(gòu)成等差數(shù)列”. 于是,他在數(shù)列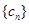 中任取三項(xiàng)
中任取三項(xiàng)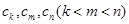 ,由
,由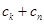 與
與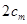 的大小關(guān)系去判斷該命題是否正確. 他將得到什么結(jié)論?
的大小關(guān)系去判斷該命題是否正確. 他將得到什么結(jié)論?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
若數(shù)列 的前n項(xiàng)和為
的前n項(xiàng)和為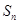 ,則下列命題:
,則下列命題:
(1)若數(shù)列 是遞增數(shù)列,則數(shù)列
是遞增數(shù)列,則數(shù)列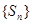 也是遞增數(shù)列;
也是遞增數(shù)列;
(2)數(shù)列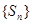 是遞增數(shù)列的充要條件是數(shù)列
是遞增數(shù)列的充要條件是數(shù)列 的各項(xiàng)均為正數(shù);
的各項(xiàng)均為正數(shù);
(3)若 是等差數(shù)列(公差
是等差數(shù)列(公差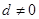 ),則
),則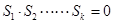 的充要條件是
的充要條件是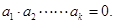
(4)若 是等比數(shù)列,則
是等比數(shù)列,則 的充要條件是
的充要條件是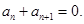
其中,正確命題的個(gè)數(shù)是( )
| A.0個(gè) | B.1個(gè) | C.2個(gè) | D.3個(gè) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
將楊輝三角中的奇數(shù)換成1,偶數(shù)換成0,得到如圖所示的0—1三角數(shù)表.從上往下數(shù),第1次全行的數(shù)都為1的是第1行,第2次全行的數(shù)都為1的是第3行,…,第 次全行的數(shù)都為1的是第 行.
次全行的數(shù)都為1的是第 行.
第1行 1 1
第2行 1 0 1
第3行 1 1 1 1
第4行 1 0 0 0 1
第5行 1 1 0 0 1 1
…………
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
對(duì)于數(shù)列 ,
,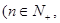
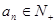 ),若
),若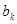 為
為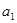 ,
,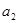 ,….,
,….,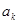 中最大值(
中最大值(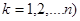 ,則稱數(shù)列
,則稱數(shù)列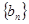 為數(shù)列
為數(shù)列 的“凸值數(shù)列”。如數(shù)列2,1,3,7,5的“凸值數(shù)列”為2,2,3,7,7;由此定義,下列說(shuō)法正確的有______
的“凸值數(shù)列”。如數(shù)列2,1,3,7,5的“凸值數(shù)列”為2,2,3,7,7;由此定義,下列說(shuō)法正確的有______
①遞減數(shù)列 的“凸值數(shù)列”是常數(shù)列;②不存在數(shù)列
的“凸值數(shù)列”是常數(shù)列;②不存在數(shù)列 ,它的“凸值數(shù)列”還是
,它的“凸值數(shù)列”還是 本身;
本身;
③任意數(shù)列 的“凸值數(shù)列”遞增數(shù)列;④“凸值數(shù)列”為1,3,3,9,的所有數(shù)列
的“凸值數(shù)列”遞增數(shù)列;④“凸值數(shù)列”為1,3,3,9,的所有數(shù)列 的個(gè)數(shù)為3.
的個(gè)數(shù)為3.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com