
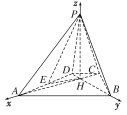
【題目】已知四棱錐P-ABCD的底面為等腰梯形, AB∥CD,AC⊥BD,垂足為H, PH是四棱錐的高,E為AD中點(diǎn),設(shè)![]()
1)證明:PE⊥BC;
2)若∠APB=∠ADB=60°,求直線PA與平面PEH所成角的正弦值.

【答案】(1)見解析;(2)![]() .
.
【解析】分析:(1)以H為原點(diǎn),HA,HB,HP所在直線分別為x,y,z軸,建立空間直角
坐標(biāo)系,利用向量法能證明PE⊥BC;
(2)求出平面PEH的法向量和![]() =(1,0,-1),利用向量法能求出直線PA與平面PEH所成角的正弦值.
=(1,0,-1),利用向量法能求出直線PA與平面PEH所成角的正弦值.
詳解:以H為原點(diǎn),HA,HB,HP所在直線分別為x,y,z軸,建立空間直角坐標(biāo)系如圖,則A(1,0,0),B(0,1,0),
(1)證明:設(shè)C(m,0,0),P(0,0,n)(m<0,n>0),則D(0,m,0),E(![]() ,
,![]() ,0).
,0).
可得![]() =(
=(![]() ,
,![]() ,-n),
,-n),![]() =(m,-1,0). 因?yàn)?/span>
=(m,-1,0). 因?yàn)?/span>![]() ·
·![]() =
=![]() -
-![]() +0=0,
+0=0,
所以PE⊥BC.
(2)由已知條件可得m=-![]() ,n=1,
,n=1,
故C(-![]() ,0,0),D(0,-
,0,0),D(0,-![]() ,0),E(
,0),E(![]() ,-
,-![]() ,0),
,0),
P(0,0,1).設(shè)n=(x,y,z)為平面PEH的法向量,
則![]() 即
即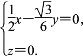
因此可以取n=(1,![]() ,0).
,0).
由![]() =(1,0,-1),可得|cos〈
=(1,0,-1),可得|cos〈![]() ,n〉|=
,n〉|=![]() ,
,
所以直線PA與平面PEH所成角的正弦值為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了解學(xué)生暑假閱讀名著的情況,一名教師對某班級的所有學(xué)生進(jìn)行了調(diào)查,調(diào)查結(jié)果如下表.
|
|
|
|
| |
男生 |
|
|
|
|
|
女生 |
|
|
|
|
|
(![]() )從這班學(xué)生中任選一名男生,一名女生,求這兩名學(xué)生閱讀名著本數(shù)之和為
)從這班學(xué)生中任選一名男生,一名女生,求這兩名學(xué)生閱讀名著本數(shù)之和為![]() 的概率?
的概率?
(![]() )若從閱讀名著不少于
)若從閱讀名著不少于![]() 本的學(xué)生中任選
本的學(xué)生中任選![]() 人,設(shè)選到的男學(xué)生人數(shù)為
人,設(shè)選到的男學(xué)生人數(shù)為![]() ,求隨機(jī)變量
,求隨機(jī)變量![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
(![]() )試判斷男學(xué)生閱讀名著本數(shù)的方差
)試判斷男學(xué)生閱讀名著本數(shù)的方差![]() 與女學(xué)生閱讀名著本數(shù)的方程
與女學(xué)生閱讀名著本數(shù)的方程![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC,AB=AC=4,BC=2,點(diǎn)D為AB延長線上一點(diǎn),BD=2,連結(jié)CD,則△BDC的面積是 , com∠BDC= .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】針對國家提出的延遲退休方案,某機(jī)構(gòu)進(jìn)行了網(wǎng)上調(diào)查,所有參與調(diào)查的人中,持“支持”、“保留”和“不支持”態(tài)度的人數(shù)如下表所示:
支持 | 保留 | 不支持 | |
|
|
|
|
|
|
|
|
(1)在所有參與調(diào)查的人中,用分層抽樣的方法抽取![]() 個(gè)人,已知從持“不支持”態(tài)度的人中抽取了
個(gè)人,已知從持“不支持”態(tài)度的人中抽取了![]() 人,求
人,求![]() 的值;
的值;
(2)在接受調(diào)查的人中,有![]() 人給這項(xiàng)活動(dòng)打出的分?jǐn)?shù)如下:
人給這項(xiàng)活動(dòng)打出的分?jǐn)?shù)如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,把這
,把這![]() 個(gè)人打出的分?jǐn)?shù)看作一個(gè)總體,從中任取一個(gè)數(shù),求該數(shù)與總體平均數(shù)之差的絕對值超過
個(gè)人打出的分?jǐn)?shù)看作一個(gè)總體,從中任取一個(gè)數(shù),求該數(shù)與總體平均數(shù)之差的絕對值超過![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某園林基地培育了一種新觀賞植物,經(jīng)過了一年的生長發(fā)育,技術(shù)人員從中抽取了部分植株的高度(單位:厘米)作為樣本(樣本容量為![]() )進(jìn)行統(tǒng)計(jì),按
)進(jìn)行統(tǒng)計(jì),按![]()
![]() 分組做出頻率分布直方圖,并作出樣本高度的莖葉圖(圖中僅列出了高度在
分組做出頻率分布直方圖,并作出樣本高度的莖葉圖(圖中僅列出了高度在![]() 的數(shù)據(jù)).
的數(shù)據(jù)).

(1)求樣本容量![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]()
(2)在選取的樣本中,從高度在80厘米以上(含80厘米)的植株中隨機(jī)抽取3株,設(shè)隨機(jī)變量![]() 表示所抽取的3株高度在
表示所抽取的3株高度在 ![]() 內(nèi)的株數(shù),求隨機(jī)變量
內(nèi)的株數(shù),求隨機(jī)變量![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)y=f(x)的導(dǎo)函數(shù)y=f′(x)的圖象如圖所示,則函數(shù)y=f(x)的圖象可能是( )
A.
B.
C.
D.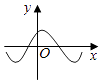
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=(x﹣ ![]() )e﹣x(x≥
)e﹣x(x≥ ![]() ).
).
(Ⅰ)求f(x)的導(dǎo)函數(shù);
(Ⅱ)求f(x)在區(qū)間[ ![]() ,+∞)上的取值范圍.
,+∞)上的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某商場經(jīng)營一批進(jìn)價(jià)是每件30元的商品,在市場銷售中發(fā)現(xiàn),此商品的銷售單價(jià)![]() 元與日銷售量
元與日銷售量![]() 件之間有如下關(guān)系
件之間有如下關(guān)系![]()
銷售單價(jià) | 30 | 40 | 45 | 50 |
日銷售量 | 60 | 30 | 15 | 0 |
(1)在平面直角坐標(biāo)系中,根據(jù)表中提供的數(shù)據(jù)描出實(shí)數(shù)對![]() 對應(yīng)的點(diǎn),并確定
對應(yīng)的點(diǎn),并確定![]() 與
與![]() 的一個(gè)函數(shù)關(guān)系式
的一個(gè)函數(shù)關(guān)系式![]() ;
;

(2)設(shè)經(jīng)營此商品的日銷售利潤為![]() 元,根據(jù)上述關(guān)系式寫出
元,根據(jù)上述關(guān)系式寫出![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式,
的函數(shù)關(guān)系式,
并指出銷售單價(jià)![]() 為多少時(shí),才能獲得最大日銷售利潤。
為多少時(shí),才能獲得最大日銷售利潤。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】三棱錐S﹣ABC及其三視圖中的正視圖和側(cè)視圖如圖所示,則該三棱錐S﹣ABC的外接球的表面積為( ) 
A.32π
B.![]()
C.![]()
D.![]() π
π
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com