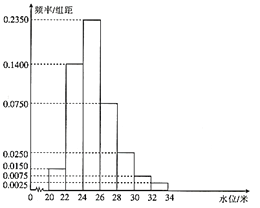
【題目】根據某水文觀測點的歷史統計數據，得到某河流水位
（單位：米）的頻率分布直方圖如下.將河流水位在
，
，
，
，
，
，
各段內的頻率作為相應段的概率，并假設每年河流水位變化互不影響.
（1）求未來4年中，至少有2年該河流水位
的概率（結果用分數表示）.
（2）已知該河流對沿河
工廠的影響如下：當
時，不會造成影響；當
時，損失50000元；當
時，損失300000元.為減少損失，工廠制定了三種應對方案.
方案一：不采取措施；
方案二：防御不超過30米的水位，需要工程費用8000元；
方案三：防御34米的最高水位，需要工程費用20000元.
試問哪種方案更好，請說明理由.
【答案】（1）
（2）
工廠應采用方案二.
【解析】
（1）根據頻率分布直方圖，先得到河流水位
的概率，再記“在未來4年中，至少有2年河流水位”為事件，即可由
求出結果；
（2）記工廠的工程費與損失費之和為
，根據題意分別求出三種方案中的期望，比較大小，取期望最小的即可.
解：（1）由頻率分布直方圖可知河流水位的概率為
.
記“在未來4年中，至少有2年河流水位”為事件，
則
.
（2）記工廠的工程費與損失費之和為（單位：元）.
①若采用方案一，則的分布列為
| 0 | 50000 | 300000 |
| 0.78 | 0.2 | 0.02 |
（元）.
②若采用方案二，則的分布列為
| 8000 | 308000 |
| 0.98 | 0.02 |
（元）.
③若采用方案三：
（元）.
因為
，所以工廠應采用方案二.
尖子生新課堂課時作業系列答案
英才計劃同步課時高效訓練系列答案科目：高中數學 來源： 題型：
【題目】下列說法正確的個數是（ ）．
①“若
,則
,
中至少有一個不小于2”的逆命題是真命題；
②命題“設
,若
,則
或
”是一個真命題；
③命題
,
,則
是
的必要不充分條件；
④命題“
,使得
”的否定是：“
，均有
”．
A.4B.3C.2D.1
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
過點
，且它的焦距是短軸長的
倍.
（1）求橢圓的方程.
（2）若
，
是橢圓上的兩個動點（，兩點不關于
軸對稱），
為坐標原點，
，
的斜率分別為
，
，問是否存在非零常數
，使當
時，
的面積
為定值？若存在，求的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
：
的左、右焦點分別為
，
，下頂點為
，橢圓的離心率是
，
的面積是
.
（1）求橢圓的標準方程.
（2）直線
與橢圓交于
，
兩點（異于點），若直線
與直線
的斜率之和為1，證明：直線恒過定點，并求出該定點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，
是過定點
且傾斜角為
的直線；在極坐標系（以坐標原點
為極點，以
軸非負半軸為極軸，取相同單位長度）中，曲線
的極坐標方程為
.
（1）寫出直線的參數方程，并將曲線的方程化為直角坐標方程；
（2）若曲線與直線相交于不同的兩點
，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設拋物線
的焦點為F，過點F作垂直于x軸的直線與拋物線交于A，B兩點，且以線段AB為直徑的圓過點
.
（1）求拋物線C的方程；
（2）設過點
的直線
分別與拋物線C交于點D，E和點G，H，且
，求四邊形
面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
