
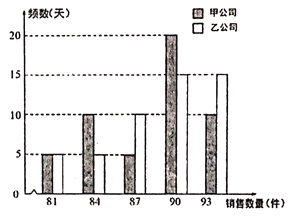
【題目】某生活超市有一專柜預(yù)代理銷售甲乙兩家公司的一種可相互替代的日常生活用品.經(jīng)過一段時間分別單獨試銷甲乙兩家公司的商品,從銷售數(shù)據(jù)中隨機各抽取50天,統(tǒng)計每日的銷售數(shù)量,得到如下的頻數(shù)分布條形圖.甲乙兩家公司給該超市的日利潤方案為:甲公司給超市每天基本費用為90元,另外每銷售一件提成1元;乙公司給超市每天的基本費用為130元,每日銷售數(shù)量不超過83件沒有提成,超過83件的部分每件提成10元.
(Ⅰ)求乙公司給超市的日利潤![]() (單位:元)與日銷售數(shù)量
(單位:元)與日銷售數(shù)量![]() 的函數(shù)關(guān)系;
的函數(shù)關(guān)系;
(Ⅱ)若將頻率視為概率,回答下列問題:
(1)求甲公司產(chǎn)品銷售數(shù)量不超過87件的概率;
(2)如果僅從日均利潤的角度考慮,請你利用所學(xué)過的統(tǒng)計學(xué)知識為超市作出抉擇,選擇哪家公司的產(chǎn)品進行銷售?并說明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)(1)
;(Ⅱ)(1)![]() ;(2)超市應(yīng)代理銷售乙公司的產(chǎn)品較為合適.
;(2)超市應(yīng)代理銷售乙公司的產(chǎn)品較為合適.
【解析】
(Ⅰ)分別在![]() 和
和![]() 兩種情況下得到關(guān)系式,進而得到結(jié)果;
兩種情況下得到關(guān)系式,進而得到結(jié)果;
(Ⅱ)(1)利用頻率的計算方式可求得對應(yīng)的概率;
(2)分別計算甲、乙兩公司給到超市的日利潤的平均數(shù),選擇平均數(shù)較大的產(chǎn)品進行銷售.
(Ⅰ)當(dāng)![]() 時,
時,![]() 元;
元;
當(dāng)![]() 時,
時,![]() ;
;
![]() 乙公司給超市的日利潤
乙公司給超市的日利潤![]() (單位:元)與銷售數(shù)量
(單位:元)與銷售數(shù)量![]() 的函數(shù)關(guān)系為:
的函數(shù)關(guān)系為:![]() .
.
(Ⅱ)(1)記事件![]() :“甲公司產(chǎn)品的銷售數(shù)量不超過87件”,
:“甲公司產(chǎn)品的銷售數(shù)量不超過87件”,
則![]() ;
;
(2)甲公司給超市的日利潤為![]() 元,
元,
則![]() 的所有可能取值為
的所有可能取值為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() (元);
(元);
設(shè)乙公司給超市的日利潤為![]() 元,
元,
則![]() 的所有可能取值為
的所有可能取值為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
則![]() (元);
(元);
![]() ,所以超市應(yīng)代理銷售乙公司的產(chǎn)品較為合適.
,所以超市應(yīng)代理銷售乙公司的產(chǎn)品較為合適.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]()
![]() 這三個條件中任選一個,補充在下面問題中,并給出解答.
這三個條件中任選一個,補充在下面問題中,并給出解答.
設(shè)等差數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,________,
,________,![]() ,若對于任意
,若對于任意![]() 都有
都有![]() ,且
,且![]() (
(![]() 為常數(shù)),求正整數(shù)
為常數(shù)),求正整數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (其中
(其中![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的參數(shù)方程為
的參數(shù)方程為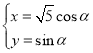 (其中
(其中![]() 為參數(shù)),以原點
為參數(shù)),以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 、
、![]() 的極坐標方程;
的極坐標方程;
(2)射線![]() :
:![]() 與曲線
與曲線![]() ,
,![]() 分別交于點
分別交于點![]() ,
,![]() (且點
(且點![]() ,
,![]() 均異于原點
均異于原點![]() ),當(dāng)
),當(dāng)![]() 時,求
時,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)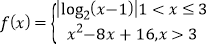 若方程f(x)=m有4個不同的實根x1,x2,x3,x4,且x1<x2<x3<x4,則(
若方程f(x)=m有4個不同的實根x1,x2,x3,x4,且x1<x2<x3<x4,則(![]() )(x3+x4)=( )
)(x3+x4)=( )
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,菱形ABCD中,![]() ,
,![]() ,O為線段CD的中點,將
,O為線段CD的中點,將![]() 沿BO折到
沿BO折到![]() 的位置,使得
的位置,使得![]() ,E為
,E為![]() 的中點.
的中點.

(1)求證:![]() ;
;
(2)求直線AE與平面![]() 所成角的正弦值
所成角的正弦值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
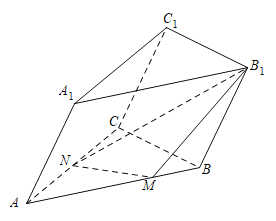
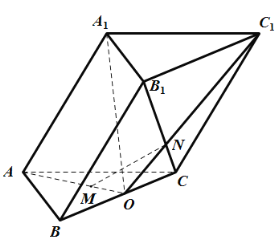
【題目】如圖所示,在三棱柱![]() 中,側(cè)面
中,側(cè)面![]() 為菱形,
為菱形,![]() ,
,![]() ,側(cè)面
,側(cè)面![]() 為正方形,平面
為正方形,平面![]() 平面
平面![]() .點
.點![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上,且
上,且![]() .
.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】每年的3月12日是植樹節(jié),某公司為了動員職工積極參加植樹造林,在植樹節(jié)期間開展植樹有獎活動,設(shè)有甲、乙兩個摸獎箱,每位植樹者植樹每滿30棵獲得一次甲箱內(nèi)摸獎機會,植樹每滿50棵獲得一次乙箱內(nèi)摸獎機會,每箱內(nèi)各有10個球(這些球除顏色外全相同),甲箱內(nèi)有紅、黃、黑三種顏色的球,其中![]() 個紅球,
個紅球,![]() 個黃球,5個黑球,乙箱內(nèi)有4個紅球和6個黃球,每次摸一個球后放回原箱,摸得紅球獎100元,黃球獎50元,摸得黑球則沒有獎金.
個黃球,5個黑球,乙箱內(nèi)有4個紅球和6個黃球,每次摸一個球后放回原箱,摸得紅球獎100元,黃球獎50元,摸得黑球則沒有獎金.
(1)經(jīng)統(tǒng)計,每人的植樹棵數(shù)![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,若其中有200位植樹者參與了抽獎,請估計植樹的棵數(shù)
,若其中有200位植樹者參與了抽獎,請估計植樹的棵數(shù)![]() 在區(qū)間
在區(qū)間![]() 內(nèi)并中獎的人數(shù)(結(jié)果四舍五入取整數(shù));
內(nèi)并中獎的人數(shù)(結(jié)果四舍五入取整數(shù));
附:若![]() ,則
,則![]() ,
,
![]() .
.
(2)若![]() ,某位植樹者獲得兩次甲箱內(nèi)摸獎機會,求中獎金額
,某位植樹者獲得兩次甲箱內(nèi)摸獎機會,求中獎金額![]() (單位:元)的分布列;
(單位:元)的分布列;
(3)某人植樹100棵,有兩種摸獎方法,
方法一:三次甲箱內(nèi)摸獎機會;
方法二:兩次乙箱內(nèi)摸獎機會;
請問:這位植樹者選哪一種方法所得獎金的期望值較大.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,斜三棱柱![]() 中,
中,![]() 是邊長為2的正三角形,
是邊長為2的正三角形,![]() 為
為![]() 的中點,
的中點,![]() 平面
平面![]() ,點
,點![]() 在
在![]() 上,
上,![]() ,
,![]() 為
為![]() 與
與![]() 的交點,且
的交點,且![]() 與平面
與平面![]() 所成的角為
所成的角為![]() .
.
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com