【題目】設
滿足約束條件
且
的最小值為7，則
＝_________.
【答案】3
【解析】
根據約束條件畫出可行域，再把目標函數轉化為
，對參數a分類討論，當
時顯然不滿足題意；當
時，直線經過可行域中的點A時，截距最小，即z有最小值，再由最小值為7，得出結果；當
時，的截距沒有最小值，即z沒有最小值；當
時，的截距沒有最大值，即z沒有最小值，綜上可得出結果.
根據約束條件畫出可行域如下：由
，可得出交點
，
由
可得，當時顯然不滿足題意；
當即
時，由可行域可知當直線經過可行域中的點A時，截距最小，即z有最小值，即
，解得
或
（舍）；
當即
時，由可行域可知的截距沒有最小值，即z沒有最小值；
當即
時，根據可行域可知的截距沒有最大值，即z沒有最小值.
綜上可知滿足條件時.
故答案為：3.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓
的長軸長為4，過點
且斜率為
的直線交橢圓于
兩點，且點
為線段
的中點
（1）求橢圓
的方程；
（2）設點
為坐標原點，過右焦點
的直線交橢圓于
兩點，（不在
軸上），求
面積
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
的圖象與
軸的交點至少有一個在原點右側．
（1）求實數
的取值范圍；
（2）令
，求
的值（其中
表示不超過
的最大整數，例如：
，
)；
（3）對（2）中的求函數
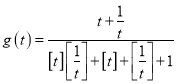的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】近期，某公交公司分別推出支付寶和微信掃碼支付乘車活動，活動設置了一段時間的推廣期，由于推廣期內優惠力度較大，吸引越來越多的人開始使用掃碼支付，某線路公交車隊統計了活動剛推出一周內每一天使用掃碼支付的人次，用x表示活動推出的天數，y表示每天使用掃碼支付的人次（單位：十人次），繪制了如圖所示的散點圖：
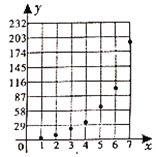
（I）根據散點圖判斷在推廣期內，
與
（c，d為為大于零的常數）哪一個適宜作為掃碼支付的人次y關于活動推出天數x的回歸方程類型？（給出判斷即可，不必說明理由）
（Ⅱ）根據（I）的判斷結果求y關于x的回歸方程，并預測活動推出第8天使用掃碼支付的人次.
參考數據：
|
|
|
|
|
|
|
4 | 62 | 1.54 | 2535 | 50.12 | 140 | 3.47 |
其中
，
附：對于一組數據
，
，…，
，其回歸直線
的斜率和截距的最小二乘估計分別為：
，
。
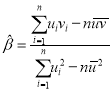查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】空氣質量AQI指數是反映空氣質量狀況指數，AQI指數值越小，表明空氣質量越好，其對應關系如表：
AQI指數值 |
|
|
|
|
|
|
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
如圖所示的是某市11月1日至20日AQI指數變化的折線圖：
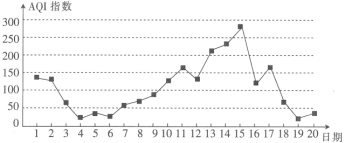
下列說法不正確的是（ ）
A.這
天中空氣質量為輕度污染的天數占
B.這天中空氣質量為優和良的天數為
天
C.這天中AQI指數值的中位數略低于
D.總體來說，該市11月上旬的空氣質量比中旬的空氣質量好
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系
中，曲線
的參數方程為
（
為參數），以坐標原點為極點，
軸正半軸為極軸建立極坐標系，直線
的極坐標方程為
.
（1）求直線與曲線公共點的極坐標；
（2）設過點
的直線
交曲線于
，
兩點，且
的中點為
，求直線的斜率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，直線
的傾斜角為
，且經過點
，以坐標原點O為極點，
軸正半軸為極軸建立極坐標系，直線
，從原點O作射線交
于點M，點N為射線OM上的點，滿足| 
，記點N的軌跡為曲線C．
（1）①設動點
，記
是直線的向上方向的單位方向向量，且
，以t為參數求直線的參數方程
②求曲線C的極坐標方程并化為直角坐標方程；
（2）設直線與曲線C交于P，Q兩點，求
的值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知兩直線方程
與
，點
在
上運動，點
在
上運動，且線段
的長為定值
.
（Ⅰ）求線段的中點
的軌跡方程；
（Ⅱ）設直線
與點的軌跡相交于
，
兩點，
為坐標原點，若
，求原點的直線
的距離的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
