
【題目】國際奧委會將于2017年9月15日在秘魯利馬召開130次會議決定2024年第33屆奧運
會舉辦地。目前德國漢堡、美國波士頓等申辦城市因市民擔心賽事費用超支而相繼退出。某機構為調查我國公民對申辦奧運會的態度,選了某小區的100位居民調查結果統計如下:
支持 | 不支持 | 合計 | |
年齡不大于50歲 | 80 | ||
年齡大于50歲 | 10 | ||
合計 | 70 | 100 |
(1)根據已有數據,把表格數據填寫完整;
(2)能否在犯錯誤的概率不超過5%的前提下認為不同年齡與支持申辦奧運無關?
(3)已知在被調查的年齡大于50歲的支持者中有5名女性,其中2位是女教師,現從這5名女性中隨機抽取3人,求至多有1位教師的概率.
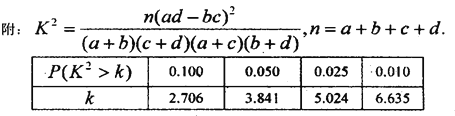
【答案】(1)見解析;(2)能在犯錯誤的概率不超過5﹪的前提下認為不同年齡與支持申辦奧運無關;(3)![]() .
.
【解析】試題分析:(1)根據條件中所給的數據填上對應的數據,即可得到列聯表;(2 )假設聾啞沒有關系,根據上一問做出的列聯表,把求得的數據代入求觀測值的公式求出觀測值,把觀測值同臨界值進行比較得到結論;(3 ) 利用列舉法,確定基本事件的個數,即利用古典概型概率公式可求出 的概率..
試題解析:
支 持 | 不 支 持 | 總 計 | |
年齡不大于50歲 | 20 | 60 | 80 |
年齡大于50歲 | 10 | 10 | 20 |
合 計 | 30 | 70 | 100 |
(1)
(2)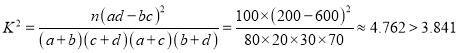
所以能在犯錯誤的概率不超過5﹪的前提下認為不同年齡與支持申辦奧運無關.
(3)記5人為a b c d e,其中a b表示教師,從5人任意抽3人的所有等可能事件是:
abc,abd,abe,acd,ace,ade,bcd,bce,bde,cde共10個,其中至多一位教師有7個基本事件:acd,ace,ade,bcd,bce,bde,cde,所以所求概率是![]() .
.


 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:高中數學 來源: 題型:
【題目】端午節吃粽子是我國的傳統習俗.設一盤中裝有10個粽子,其中豆沙粽2個,肉粽3個,白粽5個,這三種粽子的外觀完全相同.從中任意選取3個.
(1)求三種粽子各取到1個的概率;
(2)設X表示取到的豆沙粽個數,求X的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距離
的距離
(2)在線段![]() 上是否存在一點
上是否存在一點![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4;坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).在以坐標原點為極點,
為參數).在以坐標原點為極點, ![]() 軸正半軸為極軸的極坐標中,曲線
軸正半軸為極軸的極坐標中,曲線![]() .
.
(Ⅰ)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程.
的直角坐標方程.
(Ⅱ)求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知長方形ABCD中,AB=3,AD=4.現將長方形沿對角線BD折起,使AC=a,得到一個四面體A-BCD,如圖所示.
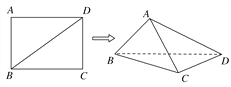
(1)試問:在折疊的過程中,直線AB與CD能否垂直?若能,求出相應a的值;若不能,請說明理由;
(2)求四面體A-BCD體積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩袋中各裝有大小相同的小球9個,其中甲袋中紅色、黑色、白色小球的個數分別為2,3,4,乙袋中紅色、黑色、白色小球的個數均為3,某人用左右手分別從甲、乙兩袋中取球.
(1)若左右手各取一球,求兩只手中所取的球顏色不同的概率;
(2)若左右手依次各取兩球,稱同一手中兩球顏色相同的取法為成功取法,記兩次取球(左右手依次各取兩球為兩次取球)的成功取法次數為隨機變量X,求X的分布列。
查看答案和解析>>
科目:高中數學 來源: 題型:
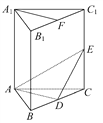
【題目】如圖,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分別是棱BC,CC1上的點(點D不同于點C),且AD⊥DE,F為B1C1的中點.
求證:(1)平面ADE⊥平面BCC1B1.
(2)直線A1F∥平面ADE.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com