Question

【題目】已知橢圓的一個(gè)焦點(diǎn)為，左、右頂點(diǎn)分別為，經(jīng)過(guò)點(diǎn)且斜率為的直線與橢圓交于兩點(diǎn)．

（1）求橢圓的方程；

（2）記與的面積分別為和，求關(guān)于的表達(dá)式，并求出當(dāng)為何值時(shí)有最大值．

Answer 1

【答案】(1) 橢圓的方程為;(2) 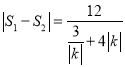當(dāng)時(shí)， 有最大值.

【解析】試題分析：

（1）由題意得，又，故可得，從而可得橢圓的方程．（2）由題意可設(shè)直線方程為，與橢圓的方程聯(lián)立消元后可得，由根與系數(shù)的關(guān)系可得．結(jié)合圖形可得=，代入后可得，最后根據(jù)基本不等式求最大值．

試題解析：

（1）∵橢圓的焦點(diǎn)為，

∴，

又，

∴，

∴橢圓的方程為．

（2）依題意知，設(shè)直線方程為，

由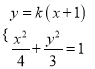消去整理得

，

∵直線與橢圓交于C,D兩點(diǎn)，

∴

且，

由題意得

，

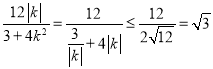∵，當(dāng)且僅當(dāng)，即時(shí)等號(hào)成立，

∴當(dāng)時(shí)， 有最大值．