
【題目】已知定義在R上的奇函數f(x),若函數f(x+1)為偶函數,且f(1)=1,則![]() f(i)=______.
f(i)=______.
【答案】1
【解析】
因為函數f(x+1)為偶函數,所以f(x)的對稱軸為x=1,再有奇函數性質得周期為4,找出一個周期的f(i)取值,進而求得.
因為函數f(x+1)為偶函數,所以f(x+1)的對稱軸為x=0,
所以f(x)的對稱軸為x=1,所以f(x+1)=f(1-x),
又因為f(x)是R上的奇函數,所以f(x+1)=f(1-x)=-f(x-1),
所以f(x+2)=-f(x),f(x+4)=-f(x+2)=f(x),所以f(x)的周期為4,
且f(1)=1,f(2)=f(-2)=-f(2),
所以f(2)=0,f(3)=f(-1)=-1,f(4)=f(0)=0,
![]() =504×[f(1)+f(2)+f(3)+f(4)]+f(1)+f(2)=1,
=504×[f(1)+f(2)+f(3)+f(4)]+f(1)+f(2)=1,
故答案為:1.


科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸的非負半軸為極軸建立極坐標系,圓
軸的非負半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與圓
與圓![]() 交于
交于![]() ,
, ![]() 兩點.
兩點.
(1)求圓![]() 的直角坐標方程及弦
的直角坐標方程及弦![]() 的長;
的長;
(2)動點![]() 在圓
在圓![]() 上(不與
上(不與![]() ,
, ![]() 重合),試求
重合),試求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】艾滋病是一種危害性極大的傳染病,由感染艾滋病病毒![]() 病毒
病毒![]() 引起,它把人體免疫系統中最重要的CD4T淋巴細胞作為主要攻擊目標,使人體喪失免疫功能
引起,它把人體免疫系統中最重要的CD4T淋巴細胞作為主要攻擊目標,使人體喪失免疫功能![]() 下表是近八年來我國艾滋病病毒感染人數統計表:
下表是近八年來我國艾滋病病毒感染人數統計表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代碼x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
感染者人數 |
|
|
|
|
|
|
| 85 |
![]() 請根據該統計表,畫出這八年我國艾滋病病毒感染人數的折線圖;
請根據該統計表,畫出這八年我國艾滋病病毒感染人數的折線圖;
![]() 請用相關系數說明:能用線性回歸模型擬合y與x的關系;
請用相關系數說明:能用線性回歸模型擬合y與x的關系;
![]() 建立y關于x的回歸方程
建立y關于x的回歸方程![]() 系數精確到
系數精確到![]() ,預測2019年我國艾滋病病毒感染人數.
,預測2019年我國艾滋病病毒感染人數.
參考數據:![]() ;
;![]() ,
,![]() ,
,![]() ,
,
參考公式:相關系數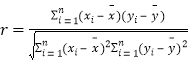 ,
,
回歸方程![]() 中,
中,![]()
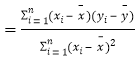 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面內與兩定點![]() ,
,![]() 連線的斜率之積等于非零常數
連線的斜率之積等于非零常數![]() 的點的軌跡,加上
的點的軌跡,加上![]() 、
、![]() 兩點所成的曲線
兩點所成的曲線![]() 可以是圓、橢圓或雙曲線,給出以下四個結論:①當
可以是圓、橢圓或雙曲線,給出以下四個結論:①當![]() 時,曲線
時,曲線![]() 是一個圓;②當
是一個圓;②當![]() 時,曲線
時,曲線![]() 的離心率為
的離心率為![]() ;③當
;③當![]() 時,曲線
時,曲線![]() 的漸近線方程為
的漸近線方程為![]() ;④當曲線
;④當曲線![]() 的焦點坐標分別為
的焦點坐標分別為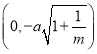 和
和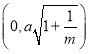 時,
時,![]() 的范圍是
的范圍是![]() .其中正確的結論序號為_______.
.其中正確的結論序號為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解一款電冰箱的使用時間和市民對這款電冰箱的購買意愿,研究人員對該款電冰箱進行了相應的抽樣調查,得到數據的統計圖表如下:
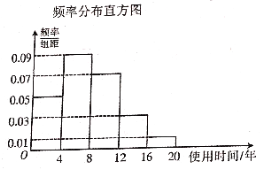
購買意愿市民年齡 | 不愿意購買該款電冰箱 | 愿意購買該款電冰箱 | 總計 |
40歲以上 | 600 | 800 | |
40歲以下 | 400 | ||
總計 | 800 |
(1)根據圖中的數據,估計該款電冰箱使用時間的中位數;
(2)完善表中數據,并據此判斷是否有![]() 的把握認為“愿意購買該款電冰箱“與“市民年齡”有關;
的把握認為“愿意購買該款電冰箱“與“市民年齡”有關;
(3)用頻率估計概率,若在該電冰箱的生產線上隨機抽取3臺,記其中使用時間不低于4年的電冰箱的臺數為![]() ,求
,求![]() 的期望.
的期望.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 上的點到右焦點F的最大距離為
上的點到右焦點F的最大距離為![]() ,離心率為
,離心率為![]() .
.
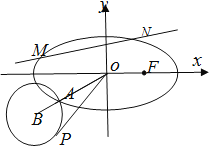
![]() 求橢圓C的方程;
求橢圓C的方程;
![]() 如圖,過點
如圖,過點![]() 的動直線l交橢圓C于M,N兩點,直線l的斜率為
的動直線l交橢圓C于M,N兩點,直線l的斜率為![]() ,A為橢圓上的一點,直線OA的斜率為
,A為橢圓上的一點,直線OA的斜率為![]() ,且
,且![]() ,B是線段OA延長線上一點,且
,B是線段OA延長線上一點,且![]() 過原點O作以B為圓心,以
過原點O作以B為圓心,以![]() 為半徑的圓B的切線,切點為
為半徑的圓B的切線,切點為![]() 令
令![]() ,求
,求![]() 取值范圍.
取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
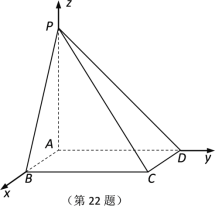
【題目】如圖所示,在四棱錐![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若點M,N分別在AB,PC上,且![]() 平面
平面![]() ,試確定點M,N的位置.
,試確定點M,N的位置.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com