
【題目】如圖1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,點E是BC邊的中點,將△ABD沿BD折起,使平面ABD⊥平面BCD,連接AE,AC,DE,得到如圖2所示的幾何體.
(Ⅰ)求證:AB⊥平面ADC;
(Ⅱ)若AD=1,二面角C﹣AB﹣D的平面角的正切值為 ![]() ,求二面角B﹣AD﹣E的余弦值.
,求二面角B﹣AD﹣E的余弦值.
【答案】(Ⅰ)解:因為平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,
又BD⊥DC,所以DC⊥平面ABD.
因為AB平面ABD,所以DC⊥AB.
又因為折疊前后均有AD⊥AB,DC∩AD=D,
所以AB⊥平面ADC
(Ⅱ)由(Ⅰ)知AB⊥平面ADC,所以二面角C﹣AB﹣D的平面角為∠CAD.
又DC⊥平面ABD,AD平面ABD,所以DC⊥AD.
依題意 ![]() .
.
因為AD=1,所以 ![]() .
.
設AB=x(x>0),則 ![]() .
.
依題意△ABD~△BDC,所以 ![]() ,即
,即  .
.
解得 ![]() ,故
,故 ![]() .
.
如圖所示,建立空間直角坐標系D﹣xyz,
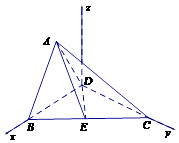
則D(0,0,0), ![]() ,
, ![]() ,
,
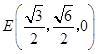 ,
, 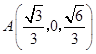 ,
,
所以 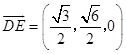 ,
, 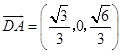 .
.
由(Ⅰ)知平面BAD的法向量 ![]() .
.
設平面ADE的法向量 ![]()
由 ![]() 得
得 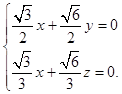
令 ![]() ,得
,得 ![]() ,
,
所以 ![]() .
.
所以 ![]() .
.
由圖可知二面角B﹣AD﹣E的平面角為銳角,
所以二面角B﹣AD﹣E的余弦值為 ![]() .
.
【解析】(Ⅰ)證明DC⊥AB.AD⊥AB即可得AB⊥平面ADC.(Ⅱ)由(Ⅰ)知AB⊥平面ADC,即二面角C﹣AB﹣D的平面角為∠CAD二面角C﹣AB﹣D的平面角的正切值為 ![]() ,解得AB,如圖所示,建立空間直角坐標系D﹣xyz,求出平面BAD的法向量
,解得AB,如圖所示,建立空間直角坐標系D﹣xyz,求出平面BAD的法向量 ![]() ,平面ADE的法向量,即可得二面角B﹣AD﹣E的余弦值
,平面ADE的法向量,即可得二面角B﹣AD﹣E的余弦值
【考點精析】解答此題的關鍵在于理解直線與平面垂直的判定的相關知識,掌握一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想.


 精英口算卡系列答案
精英口算卡系列答案 應用題點撥系列答案
應用題點撥系列答案 狀元及第系列答案
狀元及第系列答案科目:高中數學 來源: 題型:
【題目】定義:如果函數y=f(x)在定義域內給定區間[a,b]上存在x0(a<x0<b),滿足f(x0)= ![]() ,則稱函數y=f(x)是[a,b]上的“平均值函數”,x0是它的一個均值點.例如y=|x|是[﹣2,2]上的平均值函數,0就是它的均值點.若函數f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函數”,則實數m的取值范圍是 .
,則稱函數y=f(x)是[a,b]上的“平均值函數”,x0是它的一個均值點.例如y=|x|是[﹣2,2]上的平均值函數,0就是它的均值點.若函數f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函數”,則實數m的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和是Sn , 則下列四個命題中,錯誤的是( )
A.若數列{an}是公差為d的等差數列,則數列{ ![]() }的公差為
}的公差為 ![]() 的等差數列
的等差數列
B.若數列{ ![]() }是公差為d的等差數列,則數列{an}是公差為2d的等差數列
}是公差為d的等差數列,則數列{an}是公差為2d的等差數列
C.若數列{an}是等差數列,則數列的奇數項,偶數項分別構成等差數列
D.若數列{an}的奇數項,偶數項分別構成公差相等的等差數列,則{an}是等差數列
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足an= ![]() ,若從{an}中提取一個公比為q的等比數列{a
,若從{an}中提取一個公比為q的等比數列{a ![]() },其中k1=1且k1<k2<…<kn , kn∈N*,則滿足條件的最小q的值為( )
},其中k1=1且k1<k2<…<kn , kn∈N*,則滿足條件的最小q的值為( )
A.![]()
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下四個命題中其中真命題個數是( ) ①為了了解800名學生的成績,打算從中抽取一個容量為40的樣本,考慮用系統抽樣,則分段的間隔k為40;
②線性回歸直線 ![]() =
= ![]() x+
x+ ![]() 恒過樣本點的中心(
恒過樣本點的中心( ![]() ,
, ![]() );
);
③隨機變量ξ服從正態分布N(2,σ2)(σ>0),若在(﹣∞,1)內取值的概率為0.1,則在(2,3)內的概率為0.4;
④若事件M和N滿足關系P(M∪N)=P(M)+P(N),則事件M和N互斥.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】4月23日是世界讀書日,為提高學生對讀書的重視,讓更多的人暢游于書海中,從而收獲更多的知識,某高中的校學生會開展了主題為“讓閱讀成為習慣,讓思考伴隨人生”的實踐活動,校學生會實踐部的同學隨即抽查了學校的40名高一學生,通過調查它們是喜愛讀紙質書還是喜愛讀電子書,來了解在校高一學生的讀書習慣,得到如表列聯表:
喜歡讀紙質書 | 不喜歡讀紙質書 | 合計 | |
男 | 16 | 4 | 20 |
女 | 8 | 12 | 20 |
合計 | 24 | 16 | 40 |
(Ⅰ)根據如表,能否有99%的把握認為是否喜歡讀紙質書籍與性別有關系?
(Ⅱ)從被抽查的16名不喜歡讀紙質書籍的學生中隨機抽取2名學生,求抽到男生人數ξ的分布列及其數學期望E(ξ).
參考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下列的臨界值表供參考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱長為1的正方體ABCD﹣A1B1C1D1中,動點P在其表面上運動,且|PA|=x,把點的軌跡長度L=f(x)稱為“喇叭花”函數,給出下列結論: ① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④ ![]()
其中正確的結論是: . (填上你認為所有正確的結論序號)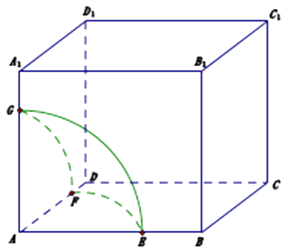
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某市擬在長為8km的道路OP的一側修建一條運動賽道,賽道的前一部分為曲線段OSM,該曲線段為函數y=Asinωx(A>0,ω>0)x∈[0,4]的圖象,且圖象的最高點為 ![]() ;賽道的后一部分為折線段MNP,為保證參賽運動員的安全,限定∠MNP=120°
;賽道的后一部分為折線段MNP,為保證參賽運動員的安全,限定∠MNP=120° 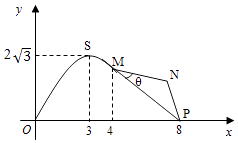
(1)求A,ω的值和M,P兩點間的距離;
(2)應如何設計,才能使折線段賽道MNP最長?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com