【題目】已知
是拋物線
上位于
軸兩側的不同兩點
（1）若
在直線
上，且使得以
為頂點的四邊形恰為正方形，求該正方形的面積.
（2）求過
、
的切線與直線
圍成的三角形面積的最小值；
課課練江蘇系列答案
名牌中學課時作業系列答案科目：高中數學 來源： 題型：
【題目】由團中央學校部、全國學聯秘書處、中國青年報社共同舉辦的2018年度全國“最美中學生”尋訪活動結果出爐啦，此項活動于2018年6月啟動，面向全國中學在校學生，通過投票方式尋訪一批在熱愛祖國、勤奮學習、熱心助人、見義勇為等方面表現突出、自覺樹立和踐行社會主義核心價值觀的“最美中學生”.現隨機抽取了30名學生的票數，繪成如圖所示的莖葉圖，若規定票數在65票以上（包括65票）定義為風華組.票數在65票以下（不包括65票）的學生定義為青春組.
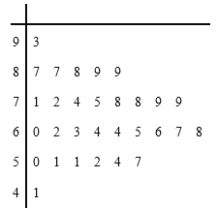
（1）如果用分層抽樣的方法從青春組和風華組中抽取5人，再從這5人中隨機抽取2人，那么至少有1人在青春組的概率是多少？
（2）用樣本估計總體，把頻率作為概率，若從該地區所有的中學（人數很多）中隨機選取4人，用
表示所選4人中青春組的人數，試寫出的分布列，并求出的數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某汽車品牌為了了解客戶對于其旗下的五種型號汽車的滿意情況，隨機抽取了一些客戶進行回訪，調查結果如下表：
汽車型號 | I | II | III | IV | V |
回訪客戶（人數） | 250 | 100 | 200 | 700 | 350 |
滿意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
滿意率是指：某種型號汽車的回訪客戶中，滿意人數與總人數的比值.
假設客戶是否滿意互相獨立，且每種型號汽車客戶對于此型號汽車滿意的概率與表格中該型號汽車的滿意率相等.
(1)從所有的回訪客戶中隨機抽取1人，求這個客戶滿意的概率；
(2)從I型號和V型號汽車的所有客戶中各隨機抽取1人，設其中滿意的人數為
，求的分布列和期望；
(3)用 “
”, “
”, “
”, “
”, “
”分別表示I, II, III, IV, V型號汽車讓客戶滿意， “
”, “
”, “
”, “
”, “
” 分別表示I, II, III, IV, V型號汽車讓客戶不滿意.寫出方差
的大小關系.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的中a1=1，a2=2，且滿足
.
（1）求數列{an}的通項公式；
（2）設bn
，記數列{bn}的前n項和為Tn，若|Tn+1|
，求n的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在三棱錐
中，
平面
，
，
，
，
為
的中點，
為
的中點.
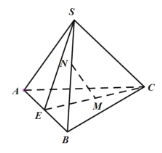
（1）證明：平面
平面
；
（2）在線段
上是否存在一點
，使
平面？若存在，指出點的位置并給出證明，若不存在，說明理由；
（3）若
，求二面角
的大小.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著手機的發展，“微信”逐漸成為人們支付購物的一種形式.某機構對“使用微信支付”的態度進行調查，隨機抽取了50人，他們年齡的頻數分布及對“使用微信支付”贊成人數如下表.
年齡 （單位：歲） |
|
|
|
|
|
|
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數 | 5 | 10 | 12 | 7 | 2 | 1 |
（Ⅰ）若以“年齡45歲為分界點”，由以上計數據完成下面
列聯表，并判斷是否有99%的把握認為“使用微信支付”的態度與人的年齡有關；
年齡不低于45歲的人數 | 年齡低于45歲的人數 | 合計 | |
贊成 | |||
不贊成 | |||
合計 |
（Ⅱ）若從年齡在
的被調查人中按照贊成與不贊成分層抽樣，抽取5人進行追蹤調查，在5人中抽取3人做專訪，求3人中不贊成使用微信支付的人數的分布列和期望值.
參考數據：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
，其中
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖為某市國慶節7天假期的商品房日認購量（單位：套）與日成交量（單位：套）的折線圖，則下面結論中正確的是( )
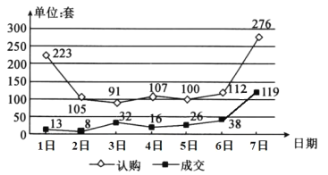
A.日成交量的中位數是16
B.日成交量超過日平均成交量的有1天
C.日認購量與日期是正相關關系
D.日認購量的方差大于日成交量的方差
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】追求人類與生存環境的和諧發展是中國特色社會主義生態文明的價值取向.為了改善空氣質量，某城市環保局隨機抽取了一年內100天的空氣質量指數（
）的檢測數據，結果統計如下：
|
|
|
|
|
|
|
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
天數 | 6 | 14 | 18 | 27 | 25 | 10 |
（1）從空氣質量指數屬于
，
的天數中任取3天，求這3天中空氣質量至少有2天為優的概率；
（2）已知某企業每天的經濟損失
（單位：元）與空氣質量指數
的關系式為
，試估計該企業一個月（按30天計算）的經濟損失的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
