
【題目】已知極點與直角坐標系的原點重合,極軸與x軸的正半軸重合,圓C的極坐標是ρ=2asinθ,直線l的參數方程是  (t為參數).
(t為參數).
(1)若a=2,M為直線l與x軸的交點,N是圓C上一動點,求|MN|的最大值;
(2)若直線l被圓C截得的弦長為 ![]() ,求a的值.
,求a的值.
【答案】
(1)解:直線l的參數方程是  ,a=2時,化為普通方程:
,a=2時,化為普通方程: ![]() (x﹣2).令y=0,解得x=2,可得M(2,0).圓C的極坐標是ρ=2asinθ,即ρ2=4ρsinθ,可得直角坐標方程:x2+y2﹣4y=0,即x2+(y﹣2)2=4.
(x﹣2).令y=0,解得x=2,可得M(2,0).圓C的極坐標是ρ=2asinθ,即ρ2=4ρsinθ,可得直角坐標方程:x2+y2﹣4y=0,即x2+(y﹣2)2=4.
|MC|=2 ![]() ,∴|MN|的最大值為2
,∴|MN|的最大值為2 ![]() +2
+2
(2)解:圓C的方程為:x2+(y﹣a)2=a2,直線l的方程為:4x+3y﹣4a=0,
圓心C到直線l的距離d= ![]() =
= ![]() .
.
∴ ![]() =2
=2 ![]() ,解得a=
,解得a= ![]()
【解析】(1)直線l的參數方程是  ,a=2時,化為普通方程:
,a=2時,化為普通方程: ![]() (x﹣2).可得M(2,0).圓C的極坐標是ρ=2asinθ,即ρ2=4ρsinθ,利用互化公式可得直角坐標方程,求出|MC|=2
(x﹣2).可得M(2,0).圓C的極坐標是ρ=2asinθ,即ρ2=4ρsinθ,利用互化公式可得直角坐標方程,求出|MC|=2 ![]() ,可得|MN|的最大值為2
,可得|MN|的最大值為2 ![]() +r.(2)圓C的方程為:x2+(y﹣a)2=a2,直線l的方程為:4x+3y﹣4a=0,利用點到直線的距離公式與弦長公式即可得出.
+r.(2)圓C的方程為:x2+(y﹣a)2=a2,直線l的方程為:4x+3y﹣4a=0,利用點到直線的距離公式與弦長公式即可得出.


 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,長方體ABCD﹣A1B1C1D1中,AA1=AB=2,AD=1點E,F,G分別是DD1 , AB,CC1的中點,則異面直線A1E與GF所成的角是( ) 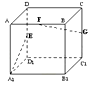
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某社區居民的家庭年收入與年支出的關系,隨機調查了該社區5戶家庭,得到如下統計數據表:
收入x(萬元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y(萬元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
根據上表可得回歸直線方程 ![]() ,其中
,其中 ![]() ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,據此估計,該社區一戶居民年收入為15萬元家庭的年支出為萬元.
,據此估計,該社區一戶居民年收入為15萬元家庭的年支出為萬元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】閱讀與探究
人教A版《普通高中課程標準實驗教科書 數學4(必修)》在第一章的小結中寫到:
將角放在直角坐標系中討論不但使角的表示有了統一的方法,而且使我們能夠借助直角坐標系中的單位圓,建立角的變化與單位圓上點的變化之間的對應關系,從而用單位圓上點的縱坐標、橫坐標來表示圓心角的正弦函數、余弦函數.因此,正弦函數、余弦函數的基本性質與圓的幾何性質(主要是對稱性)之間存在著非常緊密的聯系.例如,和單位圓相關的“勾股定理”與同角三角函數的基本關系有內在的一致性;單位圓周長為![]() 與正弦函數、余弦函數的周期為
與正弦函數、余弦函數的周期為![]() 是一致的;圓的各種對稱性與三角函數的奇偶性、誘導公式等也是一致的等等.因此,三角函數的研究過程能夠很好地體現數形結合思想.
是一致的;圓的各種對稱性與三角函數的奇偶性、誘導公式等也是一致的等等.因此,三角函數的研究過程能夠很好地體現數形結合思想.

依據上述材料,利用正切線可以討論研究得出正切函數![]() 的性質.
的性質.
比如:由圖1.2-7可知,角![]() 的終邊落在四個象限時均存在正切線;角
的終邊落在四個象限時均存在正切線;角![]() 的終邊落在
的終邊落在![]() 軸上時,其正切線縮為一個點,值為
軸上時,其正切線縮為一個點,值為![]() ;角
;角![]() 的終邊落在
的終邊落在![]() 軸上時,其正切線不存在;所以正切函數
軸上時,其正切線不存在;所以正切函數![]() 的定義域是
的定義域是![]() .
.
(1)請利用單位圓中的正切線研究得出正切函數![]() 的單調性和奇偶性;
的單調性和奇偶性;
(2)根據閱讀材料中途1.2-7,若角![]() 為銳角,求證:
為銳角,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在正方體ABCD﹣A1B1C1D1中,E、F分別是棱DD1、C1D1的中點. 
(Ⅰ)證明:平面ADC1B1⊥平面A1BE;
(Ⅱ)證明:B1F∥平面A1BE;
(Ⅲ)若正方體棱長為1,求四面體A1﹣B1BE的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過點(0,1)的直線與圓x2+y2=4相交于A、B兩點,若 ![]() ,則點P的軌跡方程是( )
,則點P的軌跡方程是( )
A.![]()
B.x2+(y﹣1)2=1
C.![]()
D.x2+(y﹣1)2=2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A是拋物線M:y2=2px(p>0)與圓C:x2+(y﹣4)2=a2在第一象限的公共點,且點A到拋物線M焦點F的距離為a,若拋物線M上一動點到其準線與到點C的距離之和的最小值為2a,O為坐標原點,則直線OA被圓C所截得的弦長為( )
A.2
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com