
【題目】![]() 年底,湖北省武漢市等多個地區陸續出現感染新型冠狀病毒肺炎的患者,為及時有效地對疫情數據進行流行病學統計分析,某地研究機構針對該地實際情況,根據該地患者是否有武漢旅行史與是否有確診病例接觸史,將新冠肺炎患者分為四類:有武漢旅行史(無接觸史),無武漢旅行史(無接觸史),有武漢旅行史(有接觸史)和無武漢旅行史(有接觸史),統計得到以下相關數據:
年底,湖北省武漢市等多個地區陸續出現感染新型冠狀病毒肺炎的患者,為及時有效地對疫情數據進行流行病學統計分析,某地研究機構針對該地實際情況,根據該地患者是否有武漢旅行史與是否有確診病例接觸史,將新冠肺炎患者分為四類:有武漢旅行史(無接觸史),無武漢旅行史(無接觸史),有武漢旅行史(有接觸史)和無武漢旅行史(有接觸史),統計得到以下相關數據:
有接觸史 | 無接觸史 | 總計 | |
有武漢旅行史 |
| ||
無武漢旅行史 |
| ||
總計 |
|
|
(1)請將上面列聯表填寫完整,并判斷能否在犯錯誤的概率不超過![]() 的前提下,認為有武漢旅行史與有確診病例接觸史有關系?
的前提下,認為有武漢旅行史與有確診病例接觸史有關系?
(2)已知在無武漢旅行史的![]() 名患者中,有
名患者中,有![]() 名無癥狀感染者.現在從無武漢旅行史的
名無癥狀感染者.現在從無武漢旅行史的![]() 名患者中,選出
名患者中,選出![]() 名進行病例研究,求
名進行病例研究,求![]() 人中至少有
人中至少有![]() 名是無癥狀感染者的概率.
名是無癥狀感染者的概率.
下面的臨界值表供參考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式: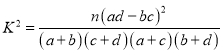 ,其中
,其中![]() .
.
【答案】(1)答案見解析,能;(2)![]() .
.
【解析】
(1)根據列聯表中的數據完善列聯表,并計算出![]() 的觀測值,結合臨界值表可得出結論;
的觀測值,結合臨界值表可得出結論;
(2)設![]() 名患者中
名患者中![]() 名無癥狀感染者記為
名無癥狀感染者記為![]() 、
、![]() ,其余
,其余![]() 名記為
名記為![]() 、
、![]() 、
、![]() 、
、![]() ,列舉出所有的基本事件,并列舉出事件“所選
,列舉出所有的基本事件,并列舉出事件“所選![]() 人中至少有
人中至少有![]() 名是無癥狀感染者”所包含的基本事件,利用古典概型的概率公式可求得所求事件的概率.
名是無癥狀感染者”所包含的基本事件,利用古典概型的概率公式可求得所求事件的概率.
(1)列聯表補充如下:
有接觸史 | 無接觸史 | 總計 | |
有武漢旅行史 |
|
|
|
無武漢旅行史 |
|
|
|
總計 |
|
|
|
![]() 的觀測值為
的觀測值為![]() ,
,
所以能在犯錯誤的概率不超過![]() 的前提下,認為有武漢旅行史與有確診病例接觸史有關系;
的前提下,認為有武漢旅行史與有確診病例接觸史有關系;
(2)設![]() 名患者中
名患者中![]() 名無癥狀感染者記為
名無癥狀感染者記為![]() 、
、![]() ,其余
,其余![]() 名記為
名記為![]() 、
、![]() 、
、![]() 、
、![]() ,
,
從![]() 人中任取
人中任取![]() 人的所有的基本事件有:
人的所有的基本事件有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 種,
種,
其中,事件“所選![]() 人中至少有
人中至少有![]() 名是無癥狀感染者”所包含的基本事件有:
名是無癥狀感染者”所包含的基本事件有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 種,
種,
因此,所求事件的概率為![]() .
.


 初中暑期銜接系列答案
初中暑期銜接系列答案科目:高中數學 來源: 題型:
【題目】很多關于整數規律的猜想都通俗易懂,吸引了大量的數學家和數學愛好者,有些猜想已經被數學家證明,如“費馬大定理”,但大多猜想還未被證明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的內容是:對于每一個正整數,如果它是奇數,則將它乘以![]() 再加1;如果它是偶數,則將它除以
再加1;如果它是偶數,則將它除以![]() ;如此循環,最終都能夠得到
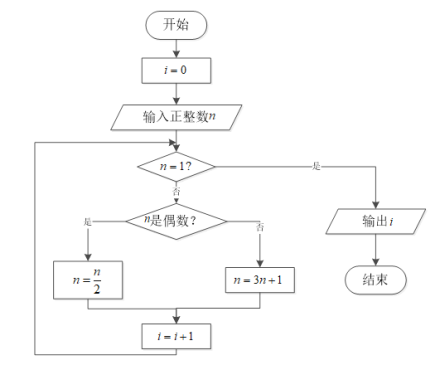
;如此循環,最終都能夠得到![]() .下圖為研究“角谷猜想”的一個程序框圖.若輸入
.下圖為研究“角谷猜想”的一個程序框圖.若輸入![]() 的值為
的值為![]() ,則輸出i的值為( )
,則輸出i的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】雙曲線![]() 的左右焦點分別為
的左右焦點分別為![]() ,
,![]() ,
,![]() 為坐標原點.
為坐標原點.![]() 為曲線
為曲線![]() 右支上的點,點
右支上的點,點![]() 在
在![]() 外角平分線上,且
外角平分線上,且![]() .若
.若![]() 恰為頂角為
恰為頂角為![]() 的等腰三角形,則該雙曲線的離心率為( )
的等腰三角形,則該雙曲線的離心率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
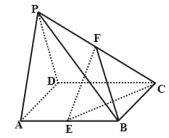
【題目】如圖所示,在四棱錐![]() 中,底面
中,底面![]() 是邊長為2的正方形,側面
是邊長為2的正方形,側面![]() 為正三角形,且面
為正三角形,且面![]() 面
面![]() ,
, ![]() 分別為棱
分別為棱![]() 的中點.
的中點.
(1)求證: ![]() 平面
平面![]() ;
;
(2)(文科)求三棱錐![]() 的體積;
的體積;
(理科)求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的短軸長為4,離心率為
的短軸長為4,離心率為![]() ,斜率不為0的直線
,斜率不為0的直線![]() 與橢圓相交于
與橢圓相交于![]() ,
,![]() 兩點(
兩點(![]() ,
,![]() 異于橢圓的頂點),且以
異于橢圓的頂點),且以![]() 為直徑的圓過橢圓的右頂點
為直徑的圓過橢圓的右頂點![]() .
.
(1)求橢圓的標準方程;
(2)直線![]() 是否過定點,如果過定點,求出該定點的坐標;如果不過定點,請說明理由.
是否過定點,如果過定點,求出該定點的坐標;如果不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線C的方程為
中,曲線C的方程為![]() ,以坐標原點O為極點,x軸的非負半軸為極軸建立極坐標系,直線l的極坐標方程為
,以坐標原點O為極點,x軸的非負半軸為極軸建立極坐標系,直線l的極坐標方程為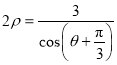 .
.
(1)求直線l的直角坐標方程和曲線C的參數方程;
(2)已知P、Q兩點分別是曲線C和直線l上的動點,且直線![]() 的傾斜角為
的傾斜角為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某超市2018年12個月的收入與支出數據的折線圖如圖所示:
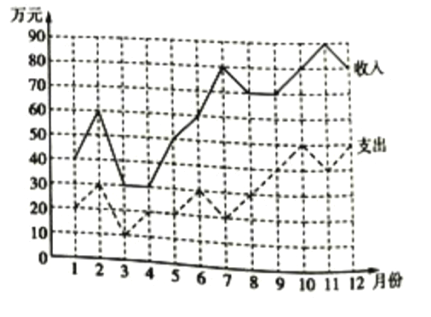
根據該折線圖可知,下列說法錯誤的是( )
A. 該超市2018年的12個月中的7月份的收益最高
B. 該超市2018年的12個月中的4月份的收益最低
C. 該超市2018年1-6月份的總收益低于2018年7-12月份的總收益
D. 該超市2018年7-12月份的總收益比2018年1-6月份的總收益增長了90萬元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,焦點為
上,焦點為![]() ,圓O的直徑為
,圓O的直徑為![]() .
.

(1)求橢圓C及圓O的標準方程;
(2)設直線l與圓O相切于第一象限內的點P,且直線l與橢圓C交于![]() 兩點.記
兩點.記![]() 的面積為
的面積為![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com