
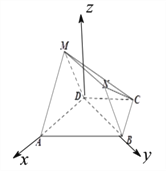
���}Ŀ����D���ڶ����w![]() �У���߅��
�У���߅��![]() ��ֱ�����Σ�
��ֱ�����Σ� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����߅��
����߅��![]() �����.
�����.

��1�����C��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2������![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹ�ö����
��ʹ�ö����![]() �Ĵ�С��
�Ĵ�С��![]() �������ڣ��_���c(di��n)
�������ڣ��_���c(di��n)![]() ��λ�ò������C��.
��λ�ò������C��.
���𰸡���1��Ҋ������2���c(di��n)![]() �龀��
�龀��![]() �����c(di��n)
�����c(di��n)
��������ԇ�}��������1���ȸ���(j��)���ɶ�����![]() �����ɾ������|(zh��)��
�����ɾ������|(zh��)��![]() ���ɾ��洹ֱ�ж�������
���ɾ��洹ֱ�ж�������![]() ��������(j��)���洹ֱ�ж������ýY(ji��)Փ ��2������(j��)�l���������gֱ������(bi��o)ϵ���O(sh��)�����c(di��n)����(bi��o)������(j��)���̽M���ƽ�淨����������(j��)������(sh��)���e�ɷ������A�ǣ�������(j��)������c�����A����Ȼ��a(b��)�P(gu��n)ϵ���c(di��n)
��������(j��)���洹ֱ�ж������ýY(ji��)Փ ��2������(j��)�l���������gֱ������(bi��o)ϵ���O(sh��)�����c(di��n)����(bi��o)������(j��)���̽M���ƽ�淨����������(j��)������(sh��)���e�ɷ������A�ǣ�������(j��)������c�����A����Ȼ��a(b��)�P(gu��n)ϵ���c(di��n)![]() ����(bi��o)�������c(di��n)
����(bi��o)�������c(di��n)![]() ���
���
ԇ�}��������1���C������ƽ��ε�֪�R(sh��)����![]() ��
�� ![]() ��
��
��![]() ��������
��������![]() ���M��
���M��![]() ������
������![]() ��ֱ�������Σ���
��ֱ�������Σ���![]() .
.
��?y��n)���߅�?/span>![]() ����Σ�
�����
����![]() .
.
��![]() ��
�� ![]() ��
�� ![]() ��
��
�ɵ� ![]() .
.
��![]() ��
��
����ƽ��![]()
![]() ƽ��
ƽ��![]() .
.
��2�������c(di��n)![]()
![]() �����
�����![]() ���c(di��n)
���c(di��n)![]() �龀��
�龀��![]() �����c(di��n).
�����c(di��n).
��(sh��)�ϣ���![]() ��ԭ�c(di��n)��
��ԭ�c(di��n)�� ![]() ��
��![]() �S��
�S�� ![]() ��
��![]() �S���^
�S���^![]() ��ƽ��
��ƽ��![]() �Ĵ�����
�Ĵ�����![]() �S���������gֱ������(bi��o)ϵ
�S���������gֱ������(bi��o)ϵ![]() ��
��
�t![]() ,
, ![]() ��
��
�O(sh��)![]() ,��
,��![]() ��
��
��![]() ����
����![]() .
.
�O(sh��)ƽ��![]() ��һ��(g��)��������
��һ��(g��)��������![]() ��
��
�t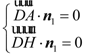 ����
����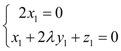 ��
��
�����O(sh��)![]() ��ȡ
��ȡ![]() .
.
ƽ��![]() ��һ��(g��)��������
��һ��(g��)��������![]() .
.
![]() �����
�����![]() �����
�����![]()
���� .
.
��� ![]() ��
��![]() ����ȥ��.
����ȥ��.
���Ԯ�(d��ng)�c(di��n)![]() �龀��
�龀��![]() �����c(di��n)�r(sh��)�������
�����c(di��n)�r(sh��)�������![]() �����
�����![]() .
.


 ȫ��(y��u)�c(di��n)����ԪӋ(j��)��ϵ�д�
ȫ��(y��u)�c(di��n)����ԪӋ(j��)��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ڡ�ABC�У�a��b��c�քe��A��B��C����߅��a+b=4����2��cosA��tan ![]() =sinA��
=sinA��
��1����߅�Lc��ֵ��
��2����E��AB�����c(di��n)����EC�ķ�����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���タ����c(di��n)������(bi��o)ԭ�c(di��n)![]() �����c(di��n)
�����c(di��n)![]() ��
��![]() �S�������S�ϣ��^���c(di��n)
�S�������S�ϣ��^���c(di��n)![]() ��б�ʞ�
��б�ʞ�![]() ��ֱ��
��ֱ��![]() �c���タ����
�c���タ����![]() ���c(di��n)���ҝM��
���c(di��n)���ҝM��![]() .
.
��1�����タ�ķ��̣�
��2����֪![]() �钁�タ��һ�c(di��n)�����c(di��n)
�钁�タ��һ�c(di��n)�����c(di��n)![]() λ��
λ��![]() �S�·���
�S�·���![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������������������܇����Ͷ�����҇�����Ѹ�Ͱl(f��)չ���������܇�����˂������ṩ�˺ܴ�ı�������Ҳ�o���еĹ��펧����һЩ���y���F(xi��n)ij���О��˽��˂����������܇��Ͷ�ŵ��J(r��n)�ɶȣ���![]() ���g�ε���Ⱥ�S�C(j��)��ȡ
���g�ε���Ⱥ�S�C(j��)��ȡ![]() ���M(j��n)����һ�������Ƿ�ٝ��Ͷ�Ź����܇���Ć����{(di��o)�飬����(j��)�{(di��o)��Y(ji��)���õ����½y(t��ng)Ӌ(j��)�������g���˔�(sh��)�l�ʷֲ�ֱ���D��
���M(j��n)����һ�������Ƿ�ٝ��Ͷ�Ź����܇���Ć����{(di��o)�飬����(j��)�{(di��o)��Y(ji��)���õ����½y(t��ng)Ӌ(j��)�������g���˔�(sh��)�l�ʷֲ�ֱ���D��
�M̖ | �ֽM | ٝ��Ͷ�ŵ��˔�(sh��) | ٝ��Ͷ�ŵ��˔�(sh��)ռ���M���l�� |
��һ�M |
|
|
|
�ڶ��M |
|
|
|
�����M |
|
|
|
���ĽM |
|
|
|
����M |
|
|
|
�����M |
|
|
|
��![]() ����
����![]() ��
�� ![]() ��
�� ![]() ��ֵ��
��ֵ��
��![]() ���ڵ��ġ��塢���M��ٝ��Ͷ�Ź����܇�������У��÷ӳ�ӵķ�����ȡ
���ڵ��ġ��塢���M��ٝ��Ͷ�Ź����܇�������У��÷ӳ�ӵķ�����ȡ![]() �˅����������܇���T܇�w�(y��n)���(d��ng)������ġ��塢���M��(y��ng)�քe��ȡ���˔�(sh��)��
�˅����������܇���T܇�w�(y��n)���(d��ng)������ġ��塢���M��(y��ng)�քe��ȡ���˔�(sh��)��
��![]() ���ڣ�
���ڣ�![]() ���г�ȡ��
���г�ȡ��![]() �����S�C(j��)�x��
�����S�C(j��)�x��![]() �������I(l��ng)�(du��)�������x�ɵ�
�������I(l��ng)�(du��)�������x�ɵ�![]() ���е���M������һ�˵ĸ��ʣ�
���е���M������һ�˵ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�c(di��n)R��x0 �� y0����D��y2=2px�ϣ���R�����c(di��n)��D���о���б�ʞ� ![]() ���^����һ�c(di��n)A������x�S�ϣ��������о�AB��AC���c(di��n)B��C�����c(di��n)����ƽ����BC���о�MN�����c(di��n)��D�����c(di��n)M��N�քe���cAB��AC�Ľ��c(di��n)����D����
���^����һ�c(di��n)A������x�S�ϣ��������о�AB��AC���c(di��n)B��C�����c(di��n)����ƽ����BC���о�MN�����c(di��n)��D�����c(di��n)M��N�քe���cAB��AC�Ľ��c(di��n)����D����
��1����B��C�Ŀv����(bi��o)s��t��ʾֱ��BC��б�ʣ�
��2���O(sh��)�����Ρ�ABC��e��S�������^����һ�c(di��n)�ăɗl�о��������l�о���ƽ���ڃ��о����c(di��n)���B�������ɵ������ν������о������Ρ������AMN������M��N�����о������Ρ��������@�ӵķ����������о������Ρ���ԇ?y��n)��á��о������Ρ�����e��Ӌ(j��)���ɒ��タ��BC�����ɵ��Ӱ���ֵ���eT��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)�E�A![]() ���ҽ��c(di��n)��
���ҽ��c(di��n)��![]() ������c(di��n)��
������c(di��n)��![]() ����֪
����֪![]() ������
������![]() ������(bi��o)ԭ�c(di��n)��
������(bi��o)ԭ�c(di��n)�� ![]() ��E�A���x����.
��E�A���x����.
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2���Ƿ����б�ʞ�2��ֱ��![]() ��ʹ�î�(d��ng)ֱ��
��ʹ�î�(d��ng)ֱ��![]() �c�E�A
�c�E�A![]() �Ѓɂ�(g��)��ͬ���c(di��n)
�Ѓɂ�(g��)��ͬ���c(di��n)![]() �r(sh��)������ֱ��
�r(sh��)������ֱ��![]() ���ҵ�һ�c(di��n)
���ҵ�һ�c(di��n)![]() ���ڙE�A
���ڙE�A![]() ���ҵ�һ�c(di��n)
���ҵ�һ�c(di��n)![]() ���M��
���M��![]() �������ڣ����ֱ��
�������ڣ����ֱ��![]() �ķ��̣��������ڣ��f������.
�ķ��̣��������ڣ��f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
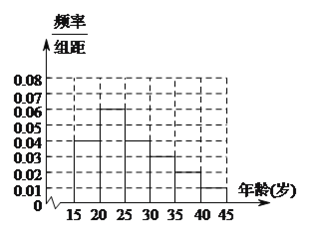
���}Ŀ��������Ҏ(gu��)��������Ҋ����������½�סլԭ�t�ϲ��ٽ��O(sh��)���]סլС�^(q��)���ѽ��ɵ�סլС�^(q��)�͆�λ��Ժ���_��������Ϣ�ھW(w��ng)��һʯ����ǧ���ˣ����N�f����һ���㣬�����˽�����_��С�^(q��)���J(r��n)ͬ�c��[25��55]�q��Ⱥ���S�C(j��)��ȡ��n���M(j��n)�І����{(di��o)�飬������(sh��)��(j��)��
�M��(sh��) | �ֽM | �J(r��n)ͬ�˔�(sh��) | �J(r��n)ͬ�˔�(sh��)ռ |
��һ�M | [25��30�� | 120 | 0.6 |
�ڶ��M | [30��35�� | 195 | p |
�����M | [35��40�� | 100 | 0.5 |
���ĽM | [40��45�� | a | 0.4 |
����M | [45��50�� | 30 | 0.3 |
�����M | [50��55�� | 15 | 0.3 |
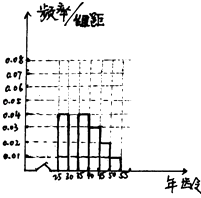
��1��������o�l�ʷֲ�ֱ���D������n��a��p��
��2�����[40��45����[45��50���ɂ�(g��)���g���еġ��J(r��n)ͬ����Ⱥ�У����ӳ�ӵķ�����9�˅��c��Մ��(hu��)��Ȼ����@9�����x2������M�L���M�L���g��[40��45����(n��i)���˔�(sh��)ӛ��Σ����S�C(j��)׃���εķֲ��к�������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����҃���ͬ�r(sh��)���a(ch��n)��(n��i)����![]() ��һ�N��������ˌ����˵����a(ch��n)�|(zh��)���M(j��n)���u�ȣ����������a(ch��n)������и���� 5 ������λ��
��һ�N��������ˌ����˵����a(ch��n)�|(zh��)���M(j��n)���u�ȣ����������a(ch��n)������и���� 5 ������λ�� ![]() �� ,
�� ,
�ף�25.44��25.43�� 25.41��25.39��25.38
�ң�25.41��25.42�� 25.41��25.39��25.42.
�����a(ch��n)�������(n��i)���ijߴ翴���l���a(ch��n)������|(zh��)���^�ߣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)f��x��=��x+1��lnx��a��x��1����
��1��������(sh��)f��x����x=e̎���о��cy�S�ཻ���c(di��n)��0��2��e������a��ֵ��
��2����(d��ng)1��x��2�r(sh��)�����C�� ![]() ��
�� ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com