
【題目】已知函數(shù)![]() .
.
(Ⅰ)當(dāng)![]() 時,求證:
時,求證: ![]() ,并指出等號成立的條件;
,并指出等號成立的條件;
(Ⅱ)求證:對任意實數(shù)![]() ,總存在實數(shù)
,總存在實數(shù)![]() ,有
,有![]() .
.
【答案】(Ⅰ)證明見解析;(Ⅱ)證明見解析
【解析】試題分析:
(Ⅰ)構(gòu)造新函數(shù)![]() ,利用導(dǎo)函數(shù)研究函數(shù)的單調(diào)性可得
,利用導(dǎo)函數(shù)研究函數(shù)的單調(diào)性可得![]() ,據(jù)此即可證得
,據(jù)此即可證得![]() .
.
(Ⅱ)原問題等價于![]() .然后分類討論當(dāng)
.然后分類討論當(dāng)![]() 時和當(dāng)
時和當(dāng)![]() 時的情況即可證得題中的結(jié)論.
時的情況即可證得題中的結(jié)論.
試題解析:
(Ⅰ)設(shè)![]()
![]() .
.
∵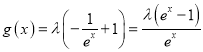 ,
,
∴當(dāng)![]() 時,
時, ![]() ,故
,故![]() 遞增;當(dāng)
遞增;當(dāng)![]() 時,
時, ![]() ,故
,故![]() 遞減.
遞減.
因此, ![]() ,即
,即![]() ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)![]() 時等號成立.
時等號成立.
(Ⅱ)解法一:“存在實數(shù)![]() ,有
,有![]() ”等價于
”等價于![]() .
.
注意到![]() .∵
.∵![]() ,
,
∴當(dāng)![]() 時,
時, ![]() ,故
,故![]() 在
在![]() 上單調(diào)遞增,從而
上單調(diào)遞增,從而![]() 成立;
成立;
當(dāng)![]() 時,令
時,令![]() ,得
,得![]() ,∴
,∴![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增
上遞增
若![]() ,即
,即![]() 時,
時, ![]() 在
在![]() 上遞增,故
上遞增,故![]() 成立;
成立;
若![]() ,即
,即![]() 時,
時, ![]() 在
在![]() 上遞增,故
上遞增,故![]() 成立;
成立;
若![]() ,即
,即![]() 時,
時, ![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,
上遞增,
故![]() 成立.
成立.
綜上所述,對任意實數(shù)![]() ,總存在實數(shù)
,總存在實數(shù)![]() ,有
,有![]() .
.
解法二:①當(dāng)![]() 時,
時, ![]() 在區(qū)間
在區(qū)間![]() 上遞增,則
上遞增,則![]() ,
,
②當(dāng)![]() 時,由(Ⅰ)可知
時,由(Ⅰ)可知![]() ;
;
③當(dāng)![]() 時,由(Ⅰ)可知
時,由(Ⅰ)可知![]()
綜上,對任意實數(shù)![]() ,總存在實數(shù)
,總存在實數(shù)![]() ,有
,有![]() .
.


 第三學(xué)期贏在暑假系列答案
第三學(xué)期贏在暑假系列答案 學(xué)練快車道快樂假期暑假作業(yè)新疆人民出版社系列答案
學(xué)練快車道快樂假期暑假作業(yè)新疆人民出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() .
.
(1)若橢圓的離心率為![]() ,且點(diǎn)
,且點(diǎn)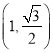 在橢圓上,①求橢圓的方程;
在橢圓上,①求橢圓的方程;
②設(shè)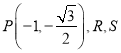 分別為橢圓
分別為橢圓![]() 的右頂點(diǎn)和上頂點(diǎn),直線
的右頂點(diǎn)和上頂點(diǎn),直線![]() 和
和![]() 與
與![]() 軸和
軸和![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)設(shè) ![]() 過
過![]() 點(diǎn)的直線
點(diǎn)的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(diǎn),且
兩點(diǎn),且![]() 均在
均在![]() 的右側(cè),
的右側(cè), ![]() ,求橢圓離心率的取值范圍.
,求橢圓離心率的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知在雙曲線 ![]() 中,F(xiàn)1 , F2分別是左右焦點(diǎn),A1 , A2 , B1 , B2分別為雙曲線的實軸與虛軸端點(diǎn),若以A1A2為直徑的圓總在菱形F1B1F2B2的內(nèi)部,則此雙曲線
中,F(xiàn)1 , F2分別是左右焦點(diǎn),A1 , A2 , B1 , B2分別為雙曲線的實軸與虛軸端點(diǎn),若以A1A2為直徑的圓總在菱形F1B1F2B2的內(nèi)部,則此雙曲線 ![]() 離心率的取值范圍是( )
離心率的取值范圍是( )
A.![]()
B.[ ![]() ,+∞)
,+∞)
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列各小題中,P是q的充要條件的是(08年山東理改編)
1)p:m<﹣2或m>6;q:y=x2+mx+m+3有兩個不同的零點(diǎn).
2)p: ![]() =1,q:y=f(x)是偶函數(shù).
=1,q:y=f(x)是偶函數(shù).
3)p:cosα=cosβ,q:tanα=tanβ.
4)p:A∩B=A,q:CUBCUA.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定義在R上的函數(shù)f(x)=2|x﹣m|﹣1(m為實數(shù))為偶函數(shù),記a=f(log0.53),b=f(log25),c=f(2m),則a,b,c的大小關(guān)系為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】觀察下列等式:32=52﹣42 , 52=132﹣122 , 72=252﹣242 , 92=412﹣402 , …照此規(guī)律,第n個等式為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)命題![]() :實數(shù)
:實數(shù)![]() 滿足
滿足![]() ,其中
,其中![]() ;命題
;命題![]() :實數(shù)
:實數(shù)![]() 滿足
滿足![]() .
.
(1)若![]() ,且
,且![]() 為真,求實數(shù)
為真,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() 是
是![]() 的充分不必要條件,求實數(shù)
的充分不必要條件,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)f(x)= ![]() (a>0,b>0).
(a>0,b>0).
(1)當(dāng)a=b=1時,證明:f(x)不是奇函數(shù);
(2)設(shè)f(x)是奇函數(shù),求a與b的值;
(3)在(2)的條件下,試證明函數(shù)f(x)的單調(diào)性,并解不等式f(1﹣m)+f(1+m2)<0.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com