
【題目】用0,1,2,3,4,5這六個數字:
(1)能組成多少個無重復數字的四位偶數?
(2)能組成多少個無重復數字且為5的倍數的五位數?
(3)能組成多少個無重復數字且比1325大的四位數?(以上各問均用數字作答)
【答案】
(1)解:符合要求的四位偶數可分為三類:
第一類:0在個位時有A53個;
第二類:2在個位時,首位從1,3,4,5中選定1個(有A41種),十位和百位從余下的數字中選(有A42種),于是有 ![]() 個;
個;
第三類:4在個位時,與第二類同理,也有 ![]() 個.
個.
由分類加法計數原理知,共有四位偶數: ![]() 個
個
(2)解:符合要求的數可分為兩類:個位數上的數字是0的五位數有A54個;個位數上的數字是5的五位數有 ![]() 個.故滿足條件的五位數的個數共有
個.故滿足條件的五位數的個數共有 ![]() 個
個
(3)解:符合要求的比1325大的四位數可分為三類:
第一類:形如2,3,4,5,共 ![]() 個;
個;
第二類:形如14□□,15□□,共有 ![]() 個;
個;
第三類:形如134□,135□,共有 ![]() 個;
個;
由分類加法計數原理知,無重復數字且比1325大的四位數共有: ![]() 個.
個.
【解析】(1)由題意符合要求的四位偶數可分為三類:0在個位,2在個位,4在個位,對每一類分別計數再求它們的和即可得到無重復數字的四位偶數的個數;(2)符合要求的數可分為兩類:個位數上的數字是0的五位數與個位數字是5的五位數,分類計數再求它們的和;(3)由題意,符合要求的比1325大的四位數可分為三類,第一類,首位比1大的數,第二類首位是1,第二位比三大的數,第三類是前兩位是13,第三位比2大的數,分類計數再求和.


 作業輔導系列答案
作業輔導系列答案科目:高中數學 來源: 題型:
【題目】已知曲線C的方程為:ax2+ay2﹣2a2x﹣4y=0(a≠0,a為常數).
(1)判斷曲線C的形狀;
(2)設曲線C分別與x軸、y軸交于點A、B(A、B不同于原點O),試判斷△AOB的面積S是否為定值?并證明你的判斷;
(3)設直線l:y=﹣2x+4與曲線C交于不同的兩點M、N,且|OM|=|ON|,求曲線C的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),其中0<α<β<π.
=(cosβ,sinβ),其中0<α<β<π.
(1)求證: ![]() 與
與 ![]() 互相垂直;
互相垂直;
(2)若k ![]() 與
與 ![]() ﹣k
﹣k ![]() 的長度相等,求β﹣α的值(k為非零的常數).
的長度相等,求β﹣α的值(k為非零的常數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某次測量中得到的A樣本數據如下:82,84,84,86,86,86,88,88,88,88.若B樣本數據恰好是A樣本數據都加2后所得數據,則A,B兩樣本的下列數字特征對應相同的是( )
A.眾數
B.平均數
C.中位數
D.標準差
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某居民區隨機抽取10個家庭,獲得第i個家庭的月收入xi(單位:千元)與月儲蓄yi(單位:千元)的數據資料,計算得 ![]() =80,
=80, ![]() =20,
=20, ![]() i=184,
i=184, ![]() =720.
=720.
(1)求家庭的月儲蓄對月收入的回歸方程;
(2)判斷月收入與月儲蓄之間是正相關還是負相關;
(3)若該居民區某家庭月收入為7千元,預測該家庭的月儲蓄.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某軍工企業生產一種精密電子儀器的固定成本為20000元,每生產一臺儀器需增加投入100元,已知總收益滿足函數:R(x)= 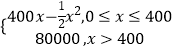 其中x是儀器的月產量.
其中x是儀器的月產量.
(1)將利潤表示為月產量的函數;
(2)當月產量為何值時,公司所獲利潤最大?最大利潤是多少元?(總收益=總成本+利潤.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,點A(0,3),直線l:y=2x﹣4.設圓C的半徑為1,圓心在l上.
(1)若圓心C也在直線y=x﹣1上,過點A作圓C的切線,求切線的方程;
(2)若圓C上存在點M,使MA=2MO,求圓心C的橫坐標a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com