【題目】已知拋物線C：x2=4y的焦點為F，過點F且斜率為1的直線與拋物線相交于M、N兩點，設直線l是拋物線C的切線，且l∥MN，P為l上一點，則 
的最小值為 ．
【答案】﹣14
【解析】解：拋物線的焦點F（0，1），∴直線MN的方程為：y=x+1．聯立方程組 
得M（2+2 
，3+2 ），N（2﹣2 ，3﹣2 ）．
設直線l的方程為y=x+b，代入x2=4y得x2﹣4x﹣4b=0，
∵直線l是拋物線C的切線，∴方程只有一解．
∴△=16+16b=0，解得b=﹣1．即l方程為：y=x﹣1．
設P（x，x﹣1）， 
=（2+2 ﹣x，4+2 ﹣x）， 
=（2﹣2 ﹣x，4﹣2 ﹣x）．
則 
=[（2﹣x）+2 ][（2﹣x）﹣2 ]+[（4﹣x）+2 ][（4﹣x）﹣2 ]=2x2﹣12x+4=2（x﹣3）2﹣14．
∴當x=3時， 取得最小值﹣14．
所以答案是：﹣14．
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=（ 
）x ， 函數g（x）=log 
x．
（1）若g（ax2+2x+1）的定義域為R，求實數a的取值范圍；
（2）當x∈[（ ）t+1 ， （ ）t]時，求函數y=[g（x）]2﹣2g（x）+2的最小值h（t）；
（3）是否存在非負實數m，n，使得函數y=log f（x2）的定義域為[m，n]，值域為[2m，2n]，若存在，求出m，n的值；若不存在，則說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）= 
，x∈R．
（1）求證：對一切實數x，f（x）=f（1﹣x）恒為定值．
（2）計算：f（﹣6）+f（﹣5）+f（﹣4）+f（﹣3）+…+f（0）+…+f（6）+f（7）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題正確的是（ ）
A.在△ABC中，角A，B，C的對邊分別是a，b，c，則a＞b是cos A＜cos B的充要條件
B.命題p：對任意的x∈R，x2+x+1＞0，則￢p：對任意的x∈R，x2+x+1≤0
C.已知p： 
＞0，則￢p： ≤0
D.存在實數x∈R，使sin x+cos x= 
成立
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，設O是平行四邊形ABCD的兩條對角線AC，BD的交點，下列向量組：
① 
與 
；② 
與 
；
③ 
與 
；④ 
與 
．
其中可作為這個平行四邊形所在平面的一組基底的是（ ）．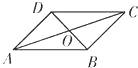
A.①②
B.③④
C.①③
D.①④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為貫徹落實教育部6部門《關于加快發展青少年校園足球的實施意見》，全面提高我市中學生的體質健康水平，培養拼搏意識和團隊精神，普及足球知識和技能，市教體局決定舉行春季校園足球聯賽．為迎接此次聯賽，甲中學選拔了20名學生組成集訓隊，現統計了這20名學生的身高，記錄入如表：（設ξ為隨機變量） 
身高（cm） | 168 | 174 | 175 | 176 | 178 | 182 | 185 | 188 |
人數 | 1 | 2 | 4 | 3 | 5 | 1 | 3 | 1 |
（1）請計算這20名學生的身高的中位數、眾數，并補充完成下面的莖葉圖；
（2）身高為185cm和188cm的四名學生分別記為A，B，C，D，現從這四名學生選2名擔任正副門將，請利用列舉法列出所有可能情況，并求學生A入選門將的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
