
��֪����(sh��) ��
��
��1���ą^(q��)�g ��(n��i)��ȡһ��(g��)��(sh��)��(sh��)
��(n��i)��ȡһ��(g��)��(sh��)��(sh��) ���O(sh��)�¼�
���O(sh��)�¼� ={����(sh��)
={����(sh��)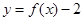 �څ^(q��)�g
�څ^(q��)�g ���Ѓɂ�(g��)��ͬ�����c(di��n)}�����¼�
���Ѓɂ�(g��)��ͬ�����c(di��n)}�����¼� �l(f��)���ĸ��ʣ�
�l(f��)���ĸ��ʣ�
��2�����B�m(x��)�S�ɴ�����(��������(g��)���Ϙ�(bi��o)ע���c(di��n)��(sh��)�քe�� ���õ����c(di��n)��(sh��)�քe��
���õ����c(di��n)��(sh��)�քe�� ��
�� ��ӛ�¼�
��ӛ�¼� {
{ ��
�� �����}�����¼�
�����}�����¼� �l(f��)���ĸ��ʣ�
�l(f��)���ĸ��ʣ�
��1��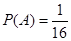 ����2��
����2��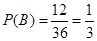 ��
��
����ԇ�}��������1������(j��)����(sh��)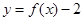 �څ^(q��)�g
�څ^(q��)�g ���Ѓɂ�(g��)��ͬ�����c(di��n)��
���Ѓɂ�(g��)��ͬ�����c(di��n)��
��֪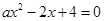 �Ѓɂ�(g��)��ͬ������
�Ѓɂ�(g��)��ͬ������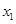 ��
��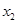 ��
��
�ɲ���ʽ�M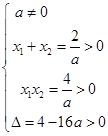
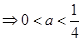 �����Îθ��͵ý⣮
�����Îθ��͵ý⣮
��2����(y��ng)�û�������ʽ�õ� ��
��
����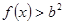 ��
��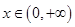 ��������õ�
��������õ�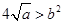 ��
��
ӑՓ��(d��ng)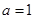 ��
��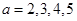 ��
��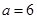 ����r��
����r��
�õ��M��l���Ļ����¼���(g��)��(sh��)���������¼�����(sh��)��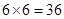 �� �ʑ�(y��ng)�ùŵ�����ʵ�Ӌ(j��)�㹫ʽ���ý⣮
�� �ʑ�(y��ng)�ùŵ�����ʵ�Ӌ(j��)�㹫ʽ���ý⣮
ԇ�}��������1��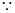 ����(sh��)
����(sh��)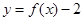 �څ^(q��)�g
�څ^(q��)�g ���Ѓɂ�(g��)��ͬ�����c(di��n)��
���Ѓɂ�(g��)��ͬ�����c(di��n)��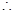
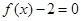 ����
����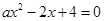 �Ѓɂ�(g��)��ͬ������
�Ѓɂ�(g��)��ͬ������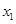 ��
��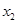
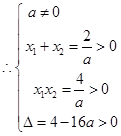
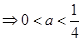 4��
4��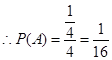 6��
6��
��2������֪��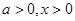 ������
������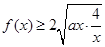 ����
����
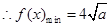 ��
�� 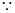
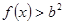 ��
��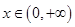 �����
����� 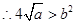
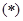 8��
8��
��(d��ng)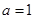 �r(sh��)��
�r(sh��)��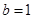 �m��
�m��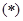 ��
��
��(d��ng)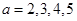 �r(sh��)��
�r(sh��)��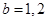 ���m��
���m��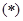 ��
��
��(d��ng)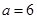 �r(sh��)��
�r(sh��)��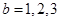 ���m��
���m��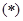 ��
��
�M��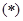 �Ļ����¼���(g��)��(sh��)��
�Ļ����¼���(g��)��(sh��)��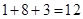 �� 10��
�� 10��
�������¼�����(sh��)��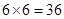 �� 11��
�� 11�� �� 12��
�� 12��
���c(di��n)���ŵ���ͣ��θ��ͣ�һԪ���η��̸��ķքe����������ʽ�đ�(y��ng)�ã�����ʽ�������(w��n)�}��


 ���D�D��(sh��)�������I(y��)�������I(y��)���ִ�W(xu��)������ϵ�д�
���D�D��(sh��)�������I(y��)�������I(y��)���ִ�W(xu��)������ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��13�֣���2011•�ؑc��ij�й��ⷿ�ķ�Դλ��A��B��C����(g��)Ƭ�^(q��)���O(sh��)ÿλ��Ո(q��ng)��ֻ��Ո(q��ng)����һ��(g��)Ƭ�^(q��)�ķ�Դ������Ո(q��ng)������һ��(g��)Ƭ�^(q��)�ķ�Դ�ǵȿ��ܵģ���ԓ�е�4λ��Ո(q��ng)���У�
��I���](m��i)������Ո(q��ng)AƬ�^(q��)��Դ�ĸ��ʣ�
��II��ÿ��(g��)Ƭ�^(q��)�ķ�Դ��������Ո(q��ng)�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
ij�ЌW(xu��)�ڸ�һ�_(k��i)�O(sh��)�˔�(sh��)�W(xu��)ʷ��4�T(m��n)��ͬ���x���n��ÿ��(g��)�W(xu��)������x�ޣ���ֻ�����xһ�T(m��n)��ԓУ��һ��3���W(xu��)���ס��ҡ�����(du��)�@4�T(m��n)��ͬ���x���n���dȤ��ͬ��
��1����ǡ��2�T(m��n)�x���n�@3��(g��)�W(xu��)�����](m��i)���x��ĸ��ʣ�
��2���O(sh��)�S�C(j��)׃��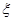 ��ס��ҡ����@����(g��)�W(xu��)���x�ޔ�(sh��)�W(xu��)ʷ�@�T(m��n)�n���˔�(sh��)����
��ס��ҡ����@����(g��)�W(xu��)���x�ޔ�(sh��)�W(xu��)ʷ�@�T(m��n)�n���˔�(sh��)����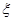 �ķֲ��м����������
�ķֲ��м����������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�Ѓ�(n��i)�д�С��ͬ��1��(g��)�t���3��(g��)�����ҺЃ�(n��i)�д�С��ͬ��2��(g��)�t���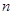 ��(g��)����
��(g��)����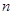 ��������(sh��)�����F(xi��n)�ļס��҃ɂ�(g��)�Ѓ�(n��i)����ȡ2��(g��)����ȡ����4��(g��)��������ĸ��ʞ�
��������(sh��)�����F(xi��n)�ļס��҃ɂ�(g��)�Ѓ�(n��i)����ȡ2��(g��)����ȡ����4��(g��)��������ĸ��ʞ�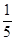 ����
����
��1��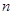 ��ֵ��
��ֵ��
��2��ȡ����4��(g��)���к���(g��)��(sh��)���ڼt��(g��)��(sh��)�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�ס��҃��˸��Sһ�����ӣ�����������w������(g��)���Ϸքe��1,2,3,4,5,6�c(di��n)���������c(di��n)��(sh��)�քe��x,y
(1)��x<y�ĸ��ʣ�
��2����5<x+y<10�ĸ��ʡ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��(du��)�� ��(g��)Ԫ�صĿ��w
��(g��)Ԫ�صĿ��w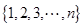 �M(j��n)�г�ӣ��Ȍ����w�ֳɃɂ�(g��)�ӿ��w
�M(j��n)�г�ӣ��Ȍ����w�ֳɃɂ�(g��)�ӿ��w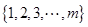 ��
��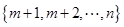 (
(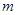 �ǽo����������(sh��)����
�ǽo����������(sh��)����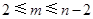 )����?g��u)�ÿ��(g��)�ӿ��w�и��S�C(j��)��ȡ
)����?g��u)�ÿ��(g��)�ӿ��w�и��S�C(j��)��ȡ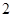 ��(g��)Ԫ�ؽM�ɘӱ�����
��(g��)Ԫ�ؽM�ɘӱ�����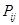 ��ʾԪ��
��ʾԪ��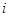 ��
��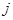 ͬ�r(sh��)���F(xi��n)�ژӱ��еĸ��ʣ�
ͬ�r(sh��)���F(xi��n)�ژӱ��еĸ��ʣ�
(1)��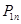 �ı��_(d��)ʽ(��
�ı��_(d��)ʽ(��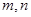 ��ʾ)��
��ʾ)��
(2)������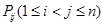 �ĺͣ�
�ĺͣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
С����ӆ��һ�݈�(b��o)�����������g���ռ���ÿ���(b��o)�����_(d��)�r(sh��)�g�Ĕ�(sh��)��(j��)�����L�Ƴ��l�ʷֲ�ֱ���D����D��ʾ��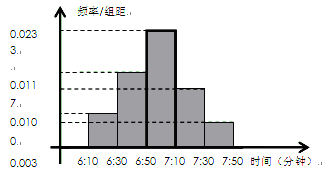
��1������(j��)�D�еĔ�(sh��)��(j��)��Ϣ���������(sh��) ����λ��(sh��)
����λ��(sh��) �����_������(sh��)��犣���
�����_������(sh��)��犣���
��2��С���ĸ��H�ϰ��x�ҵĕr(sh��)�g ������
������ ֮�g�����͈�(b��o)��ÿ����
֮�g�����͈�(b��o)��ÿ���� �r(sh��)��ǰ���С�r(sh��)��(n��i)�ш�(b��o)�����_(d��)��ÿ��(g��)�r(sh��)�g�c(di��n)���_(d��)�Ŀ�������ȣ�����С���ĸ��H���ϰ��x��ǰ���յ���(b��o)�����Q���¼�
�r(sh��)��ǰ���С�r(sh��)��(n��i)�ш�(b��o)�����_(d��)��ÿ��(g��)�r(sh��)�g�c(di��n)���_(d��)�Ŀ�������ȣ�����С���ĸ��H���ϰ��x��ǰ���յ���(b��o)�����Q���¼� ���ĸ��ʣ�
���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�ס��ҡ�����������\(y��n)��(d��ng)�T����Ŀ��(bi��o)�ĸ��ʷքe�� ��a��a(0��a��1)�����˸����һ�Σ�����Ŀ��(bi��o)�ĴΔ�(sh��)ӛ���.
��a��a(0��a��1)�����˸����һ�Σ�����Ŀ��(bi��o)�ĴΔ�(sh��)ӛ���.
(1)��εķֲ��м���(sh��)�W(xu��)������
(2)�ڸ���P(�Σ�i)(i��0��1��2��3)�У���P(�Σ�1)��ֵ�����(sh��)��(sh��)a��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
���a(ch��n)A��B�ɷNԪ�������|(zh��)�����y(c��)ԇָ��(bi��o)���֞飺ָ��(bi��o)���ڻ����82����Ʒ��С��82���Ʒ���F(xi��n)�S�C(j��)��ȡ�@�ɷNԪ����100���M(j��n)�Йz�y(c��)���z�y(c��)�Y(ji��)���y(t��ng)Ӌ(j��)���£�
| �y(c��)ԇָ��(bi��o) |  | 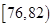 |  |  | 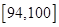 |
| Ԫ��A | 8 | 12 | 40 | 32] | 8 |
| Ԫ��B | 7 | 18 | 40 | 29 | 6 |
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com