【題目】已知動圓過定點
，且與定直線
相切，點
在
上.
（1）求動圓圓心的軌跡
的方程；
（2）試過點
且斜率為
的直線與曲線相交于
兩點。問：
能否為正三角形？
（3）過點作兩條斜率存在且互相垂直的直線
，設
與軌跡相交于
，
與軌跡相交于點
，求
的最小值.
【答案】（1）
（2）不能,理由見解析 （3）
【解析】
（1）根據題意可知動圓的圓心軌跡為拋物線,即可求得軌跡方程.
（2）寫出直線方程,聯立后可求得
兩點的坐標.設出
點坐標,根據正三角形三條邊相等,結合兩點間距離公式,可利用兩個方程分別解的縱坐標,如果兩個方程的解相等就存在這樣的正三角形,如果兩個方程的解不相等就不存在.
（3）根據斜率存在,設出兩條直線方程,聯立拋物線后根據韋達定理可得交點橫坐標的關系.將
根據向量的加法運算化簡,即可得
,根據拋物線定義可轉化為四個交點橫坐標的表達式,將韋達定理表示的式子代入,即可得關于斜率的等式,再根據基本不等式即可求得最小值.
（1）因為動圓過定點
，且與定直線
相切
所以動圓圓心
到定點與到定直線的距離相等
由拋物線定義可知,動圓圓心的軌跡是拋物線
該拋物線以為焦點,以為準線
所以動圓圓心的軌跡的方程為
（2）
不能為正三角形.理由如下:
過點
且斜率為
的直線
方程為
則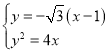
整理化簡可得
直線與曲線相交于兩點.解方程組可得兩點的坐標為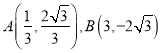
因為在
上,所以設
,且能為正三角形
則
,即滿足
當
時,由兩點間距離公式得
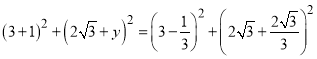
解方程可得
當
時,由兩點間距離公式得
解方程可得
因為兩個方程的解不相同,所以不存在這樣的C點,使為正三角形
即不能為正三角形.
（3）因為過點作的兩條斜率存在的直線
設直線
的斜率為
,則的方程為
,與軌跡相交于
,設
由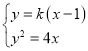
整理化簡可得
則
因為直線互相垂直,則直線
的斜率為
,其方程可設為
,與軌跡相交于點
,設
由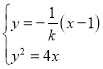
整理化簡可得
則
所以
因為直線互相垂直
則
則
由拋物線定義可知
所以
由基本不等式可知
當且僅當
,即
時取等號.即的最小值為
開心試卷期末沖刺100分系列答案
雙基同步導航訓練系列答案科目：高中數學 來源： 題型：
【題目】某大學生參加社會實踐活動，對某公司1月份至6月份銷售某種配件的銷售量及銷售單價進行了調查，銷售單價x和銷售量y之間的一組數據如下表所示：
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
銷售單價（元） | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
銷售量（件） | 11 | 10 | 8 | 6 | 5 | 14.2 |
（1）根據1至5月份的數據，求出y關于x的回歸直線方程；
（2）若由回歸直線方程得到的估計數據與剩下的檢驗數據的誤差不超過0.5元，則認為所得到的回歸直線方程是理想的，試問（1）中所得到的回歸直線方程是否理想？
（3）預計在今后的銷售中，銷售量與銷售單價仍然服從（1）中的關系，若該種機器配件的成本是2.5元/件，那么該配件的銷售單價應定為多少元才能獲得最大利潤？（注：利潤=銷售收入-成本）．
參考公式：回歸直線方程
,其中
，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某城市為了解游客人數的變化規律，提高旅游服務質量，收集并整理了
年
月至
年
月期間月接待游客量（單位：萬人）的數據，繪制了下面的折線圖.根據該折線圖，下列結論正確的是( )
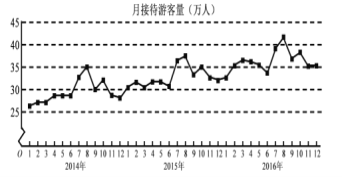
A. 月接待游客逐月增加
B. 年接待游客量逐年減少
C. 各年的月接待游客量高峰期大致在
月
D. 各年月至
月的月接待游客量相對于
月至月，波動性較小，變化比較穩定
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系中，圓
經過伸縮變換
后得到曲線
．以坐標原點為極點，
軸的正半軸為極軸，并在兩種坐標系中取相同的單位長度，建立極坐標系，直線
的極坐標方程為
．
（1）求曲線的直角坐標方程及直線的直角坐標方程；
（2）設點
是上一動點，求點到直線的距離的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列
中，
，當
時，的前
項和
滿足
（1）求的表達式；
（2）設
，數列
的前項和為
，求
；
（3）是否存在正整數
，使得
成等比數列？若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
