Question

【題目】如圖，多面體ABCDS中，面ABCD為矩形，SD⊥AD，且SD⊥AB，AD=a（a＞0），AB=2AD， ．

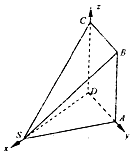
（1）求多面體ABCDS的體積；
（2）求二面角A﹣SB﹣D的余弦值．

Answer 1

【答案】
（1）解：多面體ABCCDS的體積即四棱錐S﹣ABCD的體積．

所以

（2）解：以D為原點，DS，DA，DC分別為x，y，z軸，建立空間直角坐標系，

則D（0，0，0），S（ ），B（0，a，2a），A（0，a，0），B（0，a，2a），

， ，

設面SBD的一個法向量為 =（x，y，z），

則 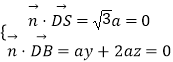，取z=1，得 =（0，﹣2，1），

又∵ ，

∴設面SAB的一個法向量為 =（x，y，z），

則 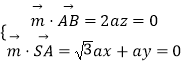，取x=1，得 ，

設二面角A﹣SB﹣D的平面角為θ，

則cosθ= = ，

所以二面角A﹣SB﹣D的余弦值為 ．

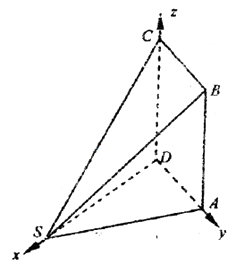
【解析】（1）多面體ABCCDS的體積即四棱錐S﹣ABCD的體積，由此能求出結果．（2）以D為原點，DS，DA，DC分別為x，y，z軸，建立空間直角坐標系，利用向量法能求出二面角A﹣SB﹣D的余弦值．