
【題目】已知函數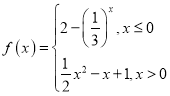 .
.
(1)當![]() 時,解不等式
時,解不等式![]() ;
;
(2)畫出該函數的圖象,并寫出該函數的單調區間(不用證明);
(3)若函數![]() 恰有3個不同零點,求實數
恰有3個不同零點,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)圖象見解析,單調遞減區間是
;(2)圖象見解析,單調遞減區間是![]() ,單調遞增區間
,單調遞增區間![]() 和
和![]() ;(3)
;(3)![]()
【解析】
(1)由![]() 時,
時,![]() ,從而可得
,從而可得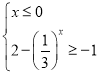 ,解不等式組即可;
,解不等式組即可;
(2)結合指數函數的性質,及二次函數的性質,可得到![]() 的單調區間,并作出函數的圖象;
的單調區間,并作出函數的圖象;
(3)由![]() 恰有3個不同零點,可知
恰有3個不同零點,可知![]() 與
與![]() 的圖象有3個不同交點,結合
的圖象有3個不同交點,結合![]() 的圖象,可求得
的圖象,可求得![]() 的取值范圍.
的取值范圍.
(1)由題意,當![]() 時,
時,![]() ,則
,則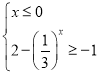 ,解得
,解得![]() .
.
(2)當![]() 時,
時,![]() ,
,
因為函數![]() 在
在![]() 上單調遞減,所以
上單調遞減,所以![]() 在
在![]() 上單調遞增.
上單調遞增.
當![]() 時,
時,![]() ,此時
,此時![]() 是對稱軸為
是對稱軸為![]() 的二次函數的一部分,所以
的二次函數的一部分,所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() .
.
作出函數![]() 的圖象,如下圖所示:
的圖象,如下圖所示:
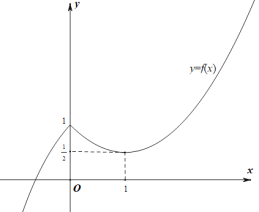
所以函數![]() 的單調遞減區間是
的單調遞減區間是![]() ,單調遞增區間是
,單調遞增區間是![]() 和
和![]() .
.
(3)函數![]() 恰有3個不同零點,即方程
恰有3個不同零點,即方程![]() 有3個不同解,
有3個不同解,
所以函數![]() 與直線
與直線![]() 的圖象有3個不同交點,
的圖象有3個不同交點,
由![]() 的圖象知,當
的圖象知,當![]() ,
,![]() 與直線
與直線![]() 的圖象有3個不同交點,
的圖象有3個不同交點,
所以實數![]() 的取值范圍是
的取值范圍是![]() .
.


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線x2=4y.

(1)求拋物線在點P(2,1)處的切線方程;
(2)若不過原點的直線l與拋物線交于A,B兩點(如圖所示),且OA⊥OB,|OA|=![]() |OB|,求直線l的斜率.
|OB|,求直線l的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省為了確定合理的階梯電價分檔方案,對全省居民用量進行了一次抽樣調查,得到居民月用電量(單位:度)的頻率分布直方圖(如圖所示),求:
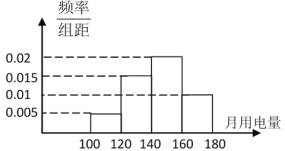
(1)若要求80%的居民能按基本檔的電量收費,則基本檔的月用電量應定為多少度?
(2)由頻率分布直方圖可估計,居民月用電量的眾數、中位數和平均數分別是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】4月16日摩拜單車進駐大連市旅順口區,綠色出行引領時尚,旅順口區對市民進行“經常使用共享單車與年齡關系”的調查統計,若將單車用戶按照年齡分為“年輕人”(20歲~39歲)和“非年輕人”(19歲及以下或者40歲及以上)兩類,抽取一個容量為200的樣本,將一周內使用的次數為6次或6次以上的稱為“經常使用單車用戶”。使用次數為5次或不足5次的稱為“不常使用單車用戶”,已知“經常使用單車用戶”有120人,其中![]() 是“年輕人”,已知“不常使用單車用戶”中有
是“年輕人”,已知“不常使用單車用戶”中有![]() 是“年輕人”.
是“年輕人”.
(1)請你根據已知的數據,填寫下列![]() 列聯表:
列聯表:
年輕人 | 非年輕人 | 合計 | |
經常使用單車用戶 | |||
不常使用單車用戶 | |||
合計 |
(2)請根據(1)中的列聯表,計算![]() 值并判斷能否有
值并判斷能否有![]() 的把握認為經常使用共享單車與年齡有關?
的把握認為經常使用共享單車與年齡有關?
(附: 
當![]() 時,有
時,有![]() 的把握說事件
的把握說事件![]() 與
與![]() 有關;當
有關;當![]() 時,有
時,有![]() 的把握說事件
的把握說事件![]() 與
與![]() 有關;當
有關;當![]() 時,認為事件
時,認為事件![]() 與
與![]() 是無關的)
是無關的)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:極坐標與參數方程
在極坐標系下,已知圓O:![]() 和直線
和直線![]()
(1)求圓O和直線l的直角坐標方程;
(2)當![]() 時,求直線l與圓O公共點的一個極坐標.
時,求直線l與圓O公共點的一個極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】要測量底部不能到達的電視塔AB的高度,在C點測得塔頂A的仰角是45°,在D點測得塔頂A的仰角是30°,并測得水平面上的∠BCD=120°,CD="40" m,則電視塔的高度為多少?
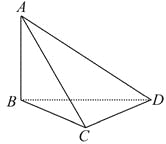
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com