
���}Ŀ����D����֪���タ![]() ��(j��ng)�^
��(j��ng)�^![]() ��
��![]() ���c(di��n)���c
���c(di��n)���c![]() �S����һ��(g��)���c(di��n)��
�S����һ��(g��)���c(di��n)��![]() ����c(di��n)��
����c(di��n)��![]() ���B�Y(ji��)
���B�Y(ji��)![]() ��
��

��1����ԓ���タ�ı��_(d��)ʽ��
��2���c(di��n)![]() ��ԓ���タ�ϵ�һ��(d��ng)�c(di��n)���c�c(di��n)
��ԓ���タ�ϵ�һ��(d��ng)�c(di��n)���c�c(di��n)![]() ��
��![]() ���غϣ����O(sh��)�c(di��n)
���غϣ����O(sh��)�c(di��n)![]() �ęM����(bi��o)��
�ęM����(bi��o)��![]() ����(d��ng)�c(di��n)
����(d��ng)�c(di��n)![]() ��ֱ��
��ֱ��![]() ���·��\(y��n)��(d��ng)�r(sh��)����
���·��\(y��n)��(d��ng)�r(sh��)����![]() ����e�����ֵ.
����e�����ֵ.
���𰸡���1��![]() ��2�����ֵ��
��2�����ֵ��![]()
��������
��1�������}�⣬�õ�![]() �����
�����![]() �����ɵó��Y(ji��)����
�����ɵó��Y(ji��)����
��2�����ɒ��タ�Ľ���ʽ���õ�![]() ���^�c(di��n)
���^�c(di��n)![]() ��
��![]() �S��ƽ�о���
�S��ƽ�о���![]() ���c(di��n)
���c(di��n)![]() �����ֱ��
�����ֱ��![]() �ķ��̞飺
�ķ��̞飺![]() ���O(sh��)�c(di��n)
���O(sh��)�c(di��n)![]() ���t�c(di��n)
���t�c(di��n)![]() ����ʾ��
����ʾ��![]() ������
������![]() ������(j��)���κ���(sh��)�����|(zh��)�����ɵó��Y(ji��)��.
������(j��)���κ���(sh��)�����|(zh��)�����ɵó��Y(ji��)��.
��1����?y��n)钁�タ![]() ��(j��ng)�^
��(j��ng)�^![]() ��
��![]() ���c(di��n)��
���c(di��n)��
����![]() ����ã�
����ã�![]() ��
��
�ʒ��タ�ı��_(d��)ʽ�飺![]() ��
��
��2����![]() ����
����![]() ���t
���t![]() ��
��![]() ��
��![]() �c(di��n)��ȥ�������c(di��n)
�c(di��n)��ȥ�������c(di��n)![]() ��
��
��D���^�c(di��n)![]() ��
��![]() �S��ƽ�о���
�S��ƽ�о���![]() ���c(di��n)
���c(di��n)![]() ��
��
��ֱ��![]() ��б�ʞ�
��б�ʞ�![]() ��
��
����ֱ��![]() �ķ��̞飺
�ķ��̞飺![]() ��
��
�O(sh��)�c(di��n)![]() ���t�c(di��n)
���t�c(di��n)![]() ��
��
����![]() ��
��
���![]()
![]() ��
��
��![]() ����
����![]() �����ֵ����(d��ng)
�����ֵ����(d��ng)![]() �r(sh��)�������ֵ��
�r(sh��)�������ֵ��![]() .
.


 �ϴ���o�����������㕽ӽ̳��Ͼ���W(xu��)������ϵ�д�
�ϴ���o�����������㕽ӽ̳��Ͼ���W(xu��)������ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����![]() ���ⲻ��ʽ
���ⲻ��ʽ![]() ��
��
��2�������ڌ�(sh��)��(sh��)![]() ��ʹ�ò���ʽ
��ʹ�ò���ʽ![]() ��������(sh��)��(sh��)
��������(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
����ӑՓ����(sh��)![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
��II���C����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��ż����(sh��)��
��ż����(sh��)��
������![]() ��ֵ��
��ֵ��
������![]() ����
����![]() ��ֵ��
��ֵ��
�����ڣ��ėl���£�������(sh��)![]() ��
��![]() ��ֻ��һ��(g��)���c(di��n)����(sh��)��(sh��)
��ֻ��һ��(g��)���c(di��n)����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����;Cˇ��(ji��)Ŀ���(qi��ng)���X���У���һ��(g��)�Α����ä�Qħ��������������^��ħ����B(t��i)���M(j��n)��ӛ����ӛס����ס�۾�����߀ԭħ����ä�Q�����˿��������棬�䌍(sh��)ԭ����ʮ�ֺ��εģ�Ҫ�W(xu��)��(hu��)ä�QҲ�Ǻ����ģ�����(j��)�{(di��o)���@ʾ���Ƿ�ϲ�gä�Qħ���c�Ԅe���P(gu��n)�������(y��n)�C�@��(g��)�Y(ji��)Փ��ij�dȤС�M�S�C(j��)��ȡ��50��ħ���ۺ����M(j��n)���{(di��o)�飬����ϲ�gä�Q��30��������22�ˣ�Ů���˔�(sh��)���õ������Բ�ϲ�gä�Q�˔�(sh��)��
��1��Ո��������![]() ��(li��n)��
��(li��n)��
ϲ�gä�Q | ��ϲ�gä�Q | ��Ӌ(j��) | |
�� | |||
Ů | |||
��Ӌ(j��) |
���Д��ܷ��ڷ��e(cu��)�`�ĸ��ʲ����^0.025��ǰ�����J(r��n)���Ƿ�ϲ�gä�Q�c�Ԅe���P(gu��n)��
��2���F(xi��n)��Ո����20����������ä�Q���Aħ����ِ���������r���±���ʾ��
�ɹ���ɕr(sh��)�g����犣� |
|
|
|
|
�˔�(sh��) | 10 | 3 | 5 | 2 |
�F(xi��n)�ı��гɹ���ɕr(sh��)�g��![]() ��
��![]() �@�ɽM��(n��i)��7�������������ȡ2�ˌ�������ä�Q��r�M(j��n)��ҕ�lӛ䛣���2�˳ɹ���ɕr(sh��)�gǡ����ͬһ�M��(n��i)�ĸ���.
�@�ɽM��(n��i)��7�������������ȡ2�ˌ�������ä�Q��r�M(j��n)��ҕ�lӛ䛣���2�˳ɹ���ɕr(sh��)�gǡ����ͬһ�M��(n��i)�ĸ���.
��������ʽ��������(sh��)��(j��)��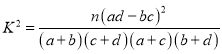 ������
������![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
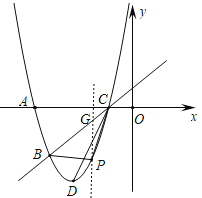
���}Ŀ����D��ʾ��![]() ��
��![]() ����ƽ�滥�ഹֱ����
����ƽ�滥�ഹֱ����![]() ��
��![]() ��
��![]() ��
��![]() �քe��
�քe��![]() ��
��![]() �����c(di��n).
�����c(di��n).

��1�����C��![]() ��
��
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() �����Q�S��
�����Q�S��![]() ����
����![]() .
.
��1����![]() ��ֵ��
��ֵ��
��2����(sh��)![]() ��
��![]() �ϵ���ֵ.
�ϵ���ֵ.
��3��������(sh��)![]() ���ҷ���
���ҷ���![]() ������(g��)�⣬��
������(g��)�⣬��![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() �ĈD��(j��ng)�^�c(di��n)
�ĈD��(j��ng)�^�c(di��n)![]() �������c(di��n)
�������c(di��n)![]() ̎���о����̞�
̎���о����̞�![]() .
.
��1����(sh��)![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����(sh��)![]() ���{(di��o)�^(q��)�g
���{(di��o)�^(q��)�g
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f(x)=![]() -ln(x+m).
-ln(x+m).
(1)�O(sh��)x=0��f(x)�ĘOֵ�c(di��n)����m����ӑՓf(x)�Ć��{(di��o)�ԣ�
��2����(d��ng)m��2�r(sh��)���C��f(x)>0.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com