Question

【題目】已知二次函數(shù)在處取得極值，且在點處的切線與直線平行．

(1）求的解析式；

(2）求函數(shù)的單調(diào)遞增區(qū)間及極值。

(3）求函數(shù)在的最值。

Answer 1

【答案】(1).

(2)增區(qū)間為,.在有極小值為0。在有極大值4/27。

（3）的最大值為2，最小值為0。

【解析】試題分析：（1）第一步，求函數(shù)的導(dǎo)數(shù)，第二步：根據(jù)處取得極值，知，根據(jù)導(dǎo)數(shù)的幾何意義知;在處的導(dǎo)數(shù)等于，解得，第三步，代入寫出，令，得到極值點，最后，解出；（2）根據(jù)（1）得到的結(jié)論，可知上的單調(diào)性，以及極值，比較端點值和極值的大小，就得到最大值和最小值.

試題解析：解：（1） 由，可得.由題設(shè)可得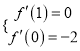

即.解得, .所以．

由題意得

所以.

令，得， .

當變化時， ， 變化情況如下表：

	單調(diào)遞增	4/27	單調(diào)遞減	0	單調(diào)遞增

所以函數(shù)的單調(diào)遞增區(qū)間為,.

（2）因為在時函數(shù)有極小值為0.在時函數(shù)有極大值．

又，

所以函數(shù)的最大值為2，最小值為0.