
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,左、右焦點為
,左、右焦點為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,且點
上,且點![]() 關于原點對稱,直線
關于原點對稱,直線![]() 的斜率的乘積為
的斜率的乘積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() 經過點
經過點![]() ,且與橢圓
,且與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,若
,若![]() ,判斷直線
,判斷直線![]() 的斜率是否為定值?若是,請求出該定值;若不是,請說明理由.
的斜率是否為定值?若是,請求出該定值;若不是,請說明理由.
科目:高中數學 來源: 題型:
【題目】隨著經濟全球化、信息化的發展,企業之間的競爭從資源的爭奪轉向人才的競爭.吸引、留住培養和用好人才成為人力資源管理的戰略目標和緊迫任務.在此背景下,某信息網站在15個城市中對剛畢業的大學生的月平均收入薪資和月平均期望薪資做了調查,數據如圖所示.
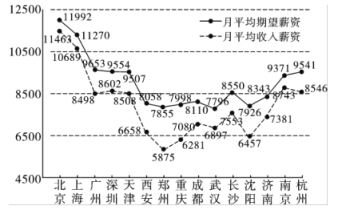
(1)若某大學畢業生從這15座城市中隨機選擇一座城市就業,求該生選中月平均收人薪資高于8000元的城市的概率;
(2)若從月平均收入薪資與月平均期望薪資之差高于1000元的城市中隨機選擇2座城市,求這2座城市的月平均期望薪資都高于8000元或都低于8000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
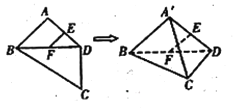
【題目】如圖,平面四邊形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中點,
中點,![]() ,
,![]() ,
,![]() ,將
,將![]() 沿對角線
沿對角線![]() 折起至
折起至![]() ,使平面
,使平面![]() ,則四面體
,則四面體![]() 中,下列結論不正確的是( )
中,下列結論不正確的是( )
A.![]() 平面
平面![]()
B.異面直線![]() 與
與![]() 所成的角為
所成的角為![]()
C.異面直線![]() 與
與![]() 所成的角為
所成的角為![]()
D.直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,設直線
,設直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,過點
,過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,
兩點,![]() 為線段
為線段![]() 的中點.
的中點.

(1)若直線![]() 的傾斜角為
的傾斜角為![]() ,求
,求![]() 的值;
的值;
(2)設直線![]() 交直線
交直線![]() 于點
于點![]() ,證明:直線
,證明:直線![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
設函數f(x)=alnx﹣bx2(x>0).
(1)若函數f(x)在x=1處于直線![]() 相切,求函數f(x)在
相切,求函數f(x)在![]() 上的最大值;
上的最大值;
(2)當b=0時,若不等式f(x)≥m+x對所有的a∈[1,![]() ],x∈[1,e2]都成立,求實數m的取值范圍.
],x∈[1,e2]都成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程是
的參數方程是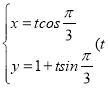 為參數),曲線
為參數),曲線![]() 的參數方程是
的參數方程是 為參數),以
為參數),以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(1)求直線![]() 和曲線
和曲線![]() 的極坐標方程;
的極坐標方程;
(2)已知射線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,射線
兩點,射線![]() 與直線
與直線![]() 交于
交于![]() 點,若
點,若![]() 的面積為1,求
的面積為1,求![]() 的值和弦長
的值和弦長![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“克拉茨猜想”又稱“![]() 猜想”,是德國數學家洛薩克拉茨在1950年世界數學家大會上公布的一個猜想:任給一個正整數
猜想”,是德國數學家洛薩克拉茨在1950年世界數學家大會上公布的一個猜想:任給一個正整數![]() ,如果
,如果![]() 是偶數,就將它減半;如果
是偶數,就將它減半;如果![]() 為奇數就將它乘3加1,不斷重復這樣的運算,經過有限步后,最終都能夠得到1.己知正整數
為奇數就將它乘3加1,不斷重復這樣的運算,經過有限步后,最終都能夠得到1.己知正整數![]() 經過6次運算后得到1,則
經過6次運算后得到1,則![]() 的值為__________.
的值為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com