
【題目】從集市上買回來的蔬菜仍存有殘留農藥,食用時需要清洗數次,統計表中的![]() 表示清洗的次數,
表示清洗的次數,![]() 表示清洗
表示清洗![]() 次后
次后![]() 千克該蔬菜殘留的農藥量(單位:微克).
千克該蔬菜殘留的農藥量(單位:微克).
|
|
|
|
|
|
|
|
|
|
|
|
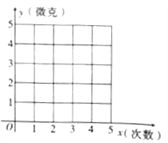
(1)在如圖的坐標系中,描出散點圖,并根據散點圖判斷,![]()
![]() 哪一個適宜作為清洗
哪一個適宜作為清洗![]() 次后
次后![]() 千克該蔬菜殘留的農藥量的回歸方程類型;(給出判斷即可,不必說明理由)
千克該蔬菜殘留的農藥量的回歸方程類型;(給出判斷即可,不必說明理由)
(2)根據判斷及下面表格中的數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
表中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3)對所求的回歸方程進行殘差分析.
附:①線性回歸方程![]() 中系數計算公式分別為
中系數計算公式分別為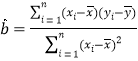 ,
,![]() ;
;
② ,
,![]() 說明模擬效果非常好;
說明模擬效果非常好;
③![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
【答案】(1)散點圖見解析,用![]() 作為清洗
作為清洗![]() 次后
次后![]() 千克該蔬菜殘留的農藥量的回歸方程類型
千克該蔬菜殘留的農藥量的回歸方程類型
(2) ![]() (3)回歸模擬的擬合效果非常好
(3)回歸模擬的擬合效果非常好
【解析】分析:(1)將表格中的點描上去,即可判斷出來散點圖類似指數型增長;
(2)按照給出的公式進行計算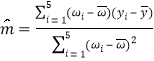 和
和![]() 即可;
即可;
(3)列出表格算出相應的值與給出的值進行比較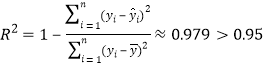 說明模擬效果非常好。
說明模擬效果非常好。
詳解:(1)散點圖如圖,
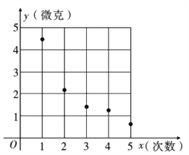
用![]() 作為清洗
作為清洗![]() 次后
次后![]() 千克該蔬菜殘留的農藥量的回歸方程類型.
千克該蔬菜殘留的農藥量的回歸方程類型.
(2)由題知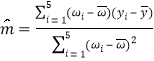
![]() ,
,
![]() ,
,
故所求的回歸方程為![]() .
.
(3)列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
所以![]() ,
,![]() ,
,![]() ,
,
所以回歸模擬的擬合效果非常好.
點晴:變量間的相關性也是每年高考的必考題,大家在拿到這類題目的時候需按照公式的需求進行運算,運算量相對較大,關注計算是重點。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某糧食店經銷小麥,年銷售量為6000千克,每千克小麥進貨價為2.8元,銷售價為3.4元,全年進貨若干次,每次的進貨量均為![]() 千克(
千克(![]() ),運費為100元/次,并且全年小麥的總存儲費用為
),運費為100元/次,并且全年小麥的總存儲費用為![]() 元.
元.
(1)用![]() (千克)表示該糧食店經銷小麥的年利潤
(千克)表示該糧食店經銷小麥的年利潤![]() (元);
(元);
(2)每次進貨量為多少千克時,能使年利潤![]() 最大?
最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形![]() 中,
中,![]() 分別是
分別是![]() 的中點將
的中點將![]() 分別沿
分別沿![]() 折起,使
折起,使![]() 重合于點
重合于點![]() .則下列結論正確的是( )
.則下列結論正確的是( )

A. ![]()
B. 平面![]()
C. 二面角![]() 的余弦值為
的余弦值為![]()
D. 點![]() 在平面
在平面![]() 上的投影是
上的投影是![]() 的外心
的外心
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為偶函數,且函數
為偶函數,且函數![]() 圖象的兩相鄰對稱軸間的距離為
圖象的兩相鄰對稱軸間的距離為![]() .
.
(1)求![]() 的值;
的值;
(2)求函數![]() 的對稱軸方程;
的對稱軸方程;
(3)當![]() 時,方程
時,方程![]() 有兩個不同的實根,求m的取值范圍。
有兩個不同的實根,求m的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】解答下列各題:
(1)已知扇形的周長為10cm,面積為4cm2,求扇形圓心角的弧度數.
(2)已知一扇形的圓心角是72°,半徑等于20cm,求扇形的面積.
(3)已知一扇形的周長為40cm,求它的半徑和圓心角取什么值時,才能使扇形的面積最大?最大面積是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某化工廠生產一種溶液,按市場要求,雜質含量不能超過0.1%,若初始溶液含雜質2%,每過濾一次可使雜質含量減少![]() .
.
(1)寫出雜質含量y與過濾次數n的函數關系式;
(2)過濾7次后的雜質含量是多少?過濾8次后的雜質含量是多少?至少應過濾幾次才能使產品達到市場要求?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為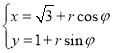 (
(![]() ,
,![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 相切;
相切;
(1)求曲線![]() 的極坐標方程與直線
的極坐標方程與直線![]() 的直角坐標方程;
的直角坐標方程;
(2)在曲線![]() 上取兩點
上取兩點![]() ,
,![]() 與原點
與原點![]() 構成
構成![]() ,且滿足
,且滿足![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com