
【題目】已知函數f(x)=﹣x3+ax在(﹣1,0)上是增函數.
(1)求實數a的取值范圍A;
(2)當a為A中最小值時,定義數列{an}滿足:a1∈(﹣1,0),且2an+1=f(an),用數學歸納法證明an∈(﹣1,0),并判斷an+1與an的大小.
【答案】
(1)解:∵f′(x)=﹣3x2+a≥0即a≥3x2在x∈(﹣1,0)恒成立,a≥3.
∴a∈[3,+∞);∴A=[3,+∞);
(2)解:用數學歸納法證明:an∈(﹣1,0).
(ⅰ)n=1時,由題設a1∈(﹣1,0);
(ⅱ)假設n=k時,ak∈(﹣1,0)
則當n=k+1時, ![]()
由(1)知:f(x)=﹣x3+3x在(﹣1,0)上是增函數,又ak∈(﹣1,0),
所以 ![]() ,
,
綜合(ⅰ)(ⅱ)得:對任意n∈N*,an∈(﹣1,0). ![]()
因為an∈(﹣1,0),所以an+1﹣an<0,即an+1<an.
【解析】(1)通過函數的導數值恒大于等于0,求實數a的取值范圍A;(2)直接利用數學歸納法證明步驟證明an∈(﹣1,0),通過作差法比較an+1與an的大小.
【考點精析】掌握利用導數研究函數的單調性和數學歸納法的定義是解答本題的根本,需要知道一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;數學歸納法是證明關于正整數n的命題的一種方法.
在這個區間單調遞減;數學歸納法是證明關于正整數n的命題的一種方法.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
在直角坐標系![]() 中圓C的參數方程為
中圓C的參數方程為![]() (
(![]() 為參數),以原點O為極點,
為參數),以原點O為極點, ![]() 軸的非負半軸為極軸建立極坐標系,直線
軸的非負半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]()
(1)求圓C的直角坐標方程及其圓心C的直角坐標;
(2)設直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)圖象的一部分如圖所示,函數g(x)=f(x+ ![]() ),則下列結論正確的是( )
),則下列結論正確的是( ) 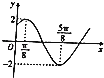
A.函數g(x)的奇函數
B.函數f(x)與g(x)的圖象均關于直線x=﹣ ![]() π對稱
π對稱
C.函數f(x)與g(x)的圖象均關于點(﹣ ![]() ,0)對稱
,0)對稱
D.函數f(x)與g(x)在區間(﹣ ![]() ,0)上均單調遞增
,0)上均單調遞增
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(sinx+ ![]() cosx)2﹣2.
cosx)2﹣2.
(1)當x∈[0, ![]() ]時,求函數f(x)的單調遞增區間;
]時,求函數f(x)的單調遞增區間;
(2)若x∈[﹣ ![]() ,
, ![]() ],求函數g(x)=
],求函數g(x)= ![]() f2(x)﹣f(x+
f2(x)﹣f(x+ ![]() )﹣1的值域.
)﹣1的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在銳角△ABC中,a、b、c分別為角A、B、C所對的邊,且 ![]() =2csinA
=2csinA
(1)確定角C的大小;
(2)若c= ![]() ,且△ABC的面積為
,且△ABC的面積為 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC A1B1C1中,D,E分別為AB,BC的中點,點F在側棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.
(1) 求證:直線DE∥平面A1C1F;
(2) 求證:平面B1DE⊥平面A1C1F.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是偶函數,且f(x+ ![]() )=f(
)=f( ![]() ﹣x),當﹣
﹣x),當﹣ ![]() ≤x≤0時,f(x)=(
≤x≤0時,f(x)=( ![]() )x﹣1,記an=f(
)x﹣1,記an=f( ![]() ),n∈N+ , 則a2046的值為( )
),n∈N+ , 則a2046的值為( )
A.1﹣ ![]()
B.1﹣ ![]()
C.![]() ﹣1
﹣1![]()
D.![]() ﹣1
﹣1![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]()
![]() .
.
(Ⅰ)若直線![]()
![]() 與曲線
與曲線![]() 和
和![]() 分別交于
分別交于![]() 兩點.設曲線
兩點.設曲線
![]() 在點
在點![]() 處的切線為
處的切線為![]() ,
, ![]() 在點
在點![]() 處的切線為
處的切線為![]() .
.
(ⅰ)當![]() 時,若
時,若![]()
![]() ,求
,求![]() 的值;
的值;
(ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅱ)設函數![]() 在其定義域內恰有兩個不同的極值點
在其定義域內恰有兩個不同的極值點![]() ,
, ![]() ,且
,且![]() .
.
若![]() ,且
,且![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com