
【題目】如圖,在四棱錐![]() 中,
中, ![]() 為等邊三角形,平面
為等邊三角形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點.
的中點.
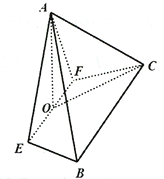
(1)求二面角![]() 的正弦值;
的正弦值;
(2)若![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】試題分析:
(1)由題意可知![]() ,
, ![]() ,
, ![]() ,據此建立空間直角坐標系,計算可得平面
,據此建立空間直角坐標系,計算可得平面![]() 的法向量為
的法向量為![]() ,且平面
,且平面![]() 的一個法向量為
的一個法向量為![]() ,據此計算可得二面角的正弦值為
,據此計算可得二面角的正弦值為![]() .
.
(2)結合(1)中的空間直角坐標系有![]() ,據此得到關于實數a的方程:
,據此得到關于實數a的方程: ![]() ,解方程有:
,解方程有: ![]() .
.
試題解析:
(1)因為![]() 是等邊三角形,
是等邊三角形, ![]() 為
為![]() 的中點,所以
的中點,所以![]() ,
,
又因為平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
取![]() 的中點
的中點![]() ,連結
,連結![]() ,
,
由題設知四邊形![]() 是等腰梯形,所以
是等腰梯形,所以![]() ,
,
由![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,
,
建立如圖所示空間直角坐標系,
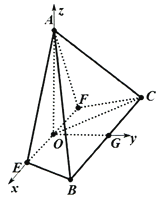
則![]() ,
, ![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
則![]() ,即
,即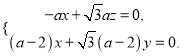
令![]() ,則
,則![]() ,于是
,于是![]() ,
,
又平面![]() 的一個法向量為
的一個法向量為![]() ,設二面角
,設二面角![]() 為
為![]() ,
,
所以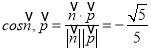 ,
, ![]() ,
,
所以二面角的正弦值為![]() .
.
(2)因為![]() 平面
平面![]() ,所以
,所以![]() ,即
,即![]() ,
,
因為![]() ,
,
所以![]() ,
,
由![]() 及
及![]() ,解得
,解得![]() .
.


科目:高中數學 來源: 題型:
【題目】“雙十一”期間,某淘寶店主對其商品的上架時間![]() (分鐘)和銷售量
(分鐘)和銷售量![]() (件)的關系作了統計,得到如下數據:
(件)的關系作了統計,得到如下數據:

經計算: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)該店主通過作散點圖,發現上架時間與銷售量線性相關,請你幫助店主求出上架時間與銷售量的線性回歸方程(保留三位小數),并預測商品上架1000分鐘時的銷售量;
(2)從這11組數據![]() 中任選2組,設
中任選2組,設![]() 且
且![]() 的數據組數為
的數據組數為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
附:線性回歸方程公式: 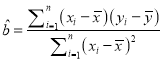 ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】網上購物逐步走進大學生活,某大學學生宿舍4人積極參加網購,大家約定:每個人通過擲一枚質地均勻的骰子決定自己去哪家購物,擲出點數為5或6的人去淘寶網購物,擲出點數小于5的人去京東商城購物,且參加者必須從淘寶網和京東商城選擇一家購物.
(1)求這4個人中恰有2人去淘寶網購物的概率;
(2)求這4個人中去淘寶網購物的人數大于去京東商城購物的人數的概率:
(3)用X,Y分別表示這4個人中去淘寶網購物的人數和去京東商城購物的人數,記![]() ,求隨機變量
,求隨機變量![]() 的分布列與數學期望
的分布列與數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b,c分別是△ABC內角A,B,C的對邊,函數f(x)=3+2![]() sin xcos x+2cos2x且f(A)=5.
sin xcos x+2cos2x且f(A)=5.
(1)求角A的大小;
(2)若a=2,求△ABC面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|ax-2|.
(1)當a=2時,解不等式f(x)>x+1;
(2)若關于x的不等式f(x)+f(-x)< ![]() 有實數解,求m的取值范圍.
有實數解,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() 的一個焦點與拋物線y2=-4x的焦點相同,且橢圓C上一點與橢圓C的左,右焦點F1,F2構成的三角形的周長為
的一個焦點與拋物線y2=-4x的焦點相同,且橢圓C上一點與橢圓C的左,右焦點F1,F2構成的三角形的周長為![]() .
.
(1)求橢圓C的方程;
(2)若直線l:y=kx+m(k,m∈R)與橢圓C交于A,B兩點,O為坐標原點,△AOB的重心G滿足: ![]() ,求實數m的取值范圍.
,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)及其導數f′(x),若存在x0,使得f(x0)=f′(x0),則稱x0是f(x)的一個“巧值點”,則下列函數中有“巧值點”的是________.
①f(x)=x2;②f(x)=e-x;③f(x)=lnx;④f(x)=tanx;⑤![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (其中
(其中![]() 為參數),以
為參數),以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() (其中
(其中![]() 為常數).
為常數).
(1)若直線![]() 與曲線
與曲線![]() 恰好有一個公共點,求實數
恰好有一個公共點,求實數![]() 的值;
的值;
(2)若![]() ,求直線
,求直線![]() 被曲線
被曲線![]() 截得的弦長.
截得的弦長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com