【題目】已知函數 
（1）判斷函數 
的單調性并給出證明；
（2）若存在實數 
使函數 是奇函數，求 ；
（3）對于(2)中的 ，若 
，當 
時恒成立，求 
的最大值．
【答案】
（1）解：不論a為何實數，f(x)在定義域上單調遞增．
證明：設x1 ， x2∈R，且x1<x2 ，
則 
由 
可知 
，所以 
, 
所以 
所以由定義可知，不論 
為何值， 
在定義域上單調遞增
（2）解：由f(0)＝a－1＝0得a＝1，
經驗證，當a＝1時， f(x)是奇函數
（3）解：由條件可得： m 
2x 
＝(2x＋1)＋ 
－3恒成立．m (2x＋1)＋ －3的最小值，x∈[2,3]．
設t＝2x＋1，則t∈[5,9]，函數g(t)＝t＋ 
－3在[5,9]上單調遞增，
所以g(t)的最小值是g(5)＝ 
，
所以m ，即m的最大值是
【解析】本題主要考查函數單調性以及函數 的奇偶性和函數最值的問題。（1）要判斷函數的單調性并證明，主要利用函數的單調性的定義來進行證明，注意要化成乘積形式進行求解。（2）函數的奇偶性的判斷，注意函數的定義域中包含原點的函數一定過原點。（3）因為有不等式恒成立，把不等式轉化為m ≤ (2x＋1)＋
的形式，求函數的最小值即可。
【考點精析】通過靈活運用函數單調性的性質和函數的奇偶性，掌握函數的單調區間只能是其定義域的子區間 ,不能把單調性相同的區間和在一起寫成其并集；偶函數的圖象關于y軸對稱；奇函數的圖象關于原點對稱即可以解答此題．
全能測控期末小狀元系列答案科目：高中數學 來源： 題型：
【題目】設 
與 
是定義在同一區間 
上的兩個函數，若函數 
（ 
為函數 的導函數），在 上有且只有兩個不同的零點，則稱 是 在 上的“關聯函數”，若 
，是 
在 
上的“關聯函數”，則實數 
的取值范圍是（ ）．
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校組織學生參加英語測試，成績的頻率分布直方圖如圖，數據的分組依次為[20，40），[40，60），[60，80），[80，100]，若低于60分的人數是15人，則該班的學生人數是（ ） 
A.45
B.50
C.55
D.60
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在如圖所示的幾何體中，平面 
平面 
，四邊形 為平行四邊形， 
， 
， 
， 
.
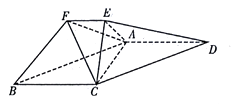
（1）求證： 
平面 
；
（2）求 
到平面 的距離；
（3）求三棱錐 
的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線C：y2=2px（p＞0）的焦點為F，點M（2，m）為其上一點，且|MF|=4． 
（1）求p與m的值；
（2）如圖，過點F作直線l交拋物線于A、B兩點，求直線OA、OB的斜率之積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝(m2－m－1)x－5m－3，m為何值時，f(x)：
(1)是冪函數；
(2)是正比例函數；
(3)是反比例函數；
(4)是二次函數．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
E是PC的中點．求證：
（Ⅰ）CD⊥AE；
（Ⅱ）PD⊥平面ABE．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】知f（x）=xlnx，g（x）=﹣x2+ax﹣3．
（1）求函數f（x）在區間[t，t+2]（t＞0）上的最小值；
（2）對一切實數x∈（0，+∞），2f（x）≥g（x）恒成立，求實數a的取值范圍；
（3）證明對一切x∈（0，+∞），lnx＞ 
恒成立．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
