Question

【題目】已知函數.

（1）指出函數的基本性質：定義域，奇偶性，單調性，值域（結論不需證明），并作出函數的圖象；

（2）若關于的不等式恒成立，求實數的取值范圍；

（3）若關于的方程恰有個不同的實數解，求實數的取值范圍.

Answer 1

【答案】（1）定義域：，是偶函數，在區間和上單調遞增，在區間和上單調遞減，值域為，作圖見解析；（2）；（3）.

【解析】

（1）將函數表示為分段函數，利用基本初等函數的基本性質可得出函數的定義域、奇偶性、單調性和值域，并結合解析式作出該函數的圖象；

（2）令，可得出不等式在恒成立，然后利用參變量分離法得出，求出函數的最大值，即可得出實數的取值范圍；

（3）令，結合題意可得知關于的方程的兩根，，然后利用二次函數的零點分布列出關于、的不等式組，即可求出實數的取值范圍.

（1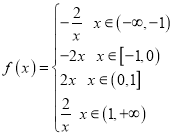），，函數是偶函數，

在區間和上單調遞增，在區間和上單調遞減，

函數的最大值是，無最小值，值域為.

作圖如下：

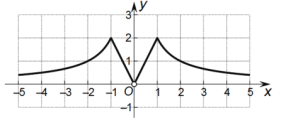
（2）因為關于的不等式恒成立，

令，則，即不等式在恒成立.

當時，因為，所以.

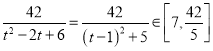又，所以；

（3）關于的方程恰有個不同的實數解即有個不同的解，如下圖所示：

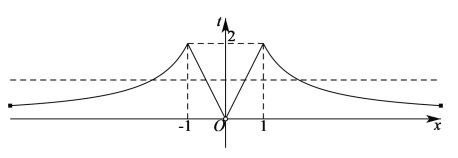
當時，方程有四個根；當時，方程有兩個根；

當或時， 方程無解.

設方程的兩根分別為、，則，.

令，則.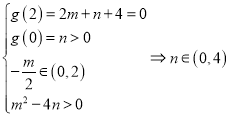

因此，實數的取值范圍是.