
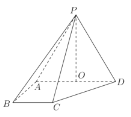
【題目】如圖,在四棱錐![]() 中,
中,![]() 為
為![]() 中點,側棱
中點,側棱![]() ,底面
,底面![]() 為直角梯形,其中
為直角梯形,其中![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 、
、![]() 分別是線段
分別是線段![]() 、
、![]() 上的動點,且
上的動點,且![]() .
.
(1)求證:![]() 平面
平面![]() ;
;
(2)當三棱錐![]() 的體積取最大值時,求
的體積取最大值時,求![]() 到平面
到平面![]() 的距離;
的距離;
(3)在(2)的條件下求![]() 與平面
與平面![]() 所成角.
所成角.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)證明![]() 和
和![]() 即可;
即可;
(2)根據體積最值關系求出![]() 分別為
分別為![]() 的中點,建立空間直角坐標系,求出平面
的中點,建立空間直角坐標系,求出平面![]() 的法向量,利用公式
的法向量,利用公式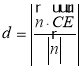 求距離;
求距離;
(3)結合第(2)問的法向量利用公式![]() 即可求出線面角.
即可求出線面角.
(1)在![]() 中,
中,![]() 為
為![]() 中點,側棱
中點,側棱![]() ,所以
,所以![]() ,
,
又因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
![]() 是平面
是平面![]() 內兩條相交直線,
內兩條相交直線,
所以![]() 平面
平面![]() ;
;
(2)![]() ,即
,即![]() ,
,
![]() ,所以
,所以![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
連接![]() ,
,
設![]() ,則
,則![]() ,由(1)
,由(1)![]() 平面
平面![]() ,
,
所以![]() 是點
是點![]() 到平面
到平面![]() 的距離,
的距離,
所以三棱錐![]() 的體積
的體積
![]()
![]()
![]() ,
,![]() ,當
,當![]() 時,取得最大值
時,取得最大值![]()
此時![]() 分別為
分別為![]() 的中點,
的中點,
![]() ,所以四邊形
,所以四邊形![]() 是平行四邊形,
是平行四邊形,![]() ,
,
所以四邊形![]() 是正方形,
是正方形,![]() ,
,
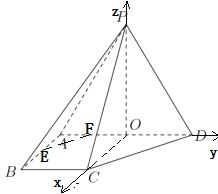
以![]() 為原點,
為原點,![]() 方向為
方向為![]() 軸正方向建立空間直角坐標系,如圖所示:
軸正方向建立空間直角坐標系,如圖所示:
則![]() ,
,
![]() ,
,
設平面![]() 的法向量
的法向量![]() ,則
,則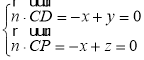 ,
,
取![]() ,則
,則![]() ,
,
所以點![]() 到平面
到平面![]() 的距離
的距離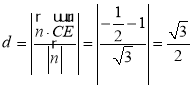 ;
;
(3)設![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,
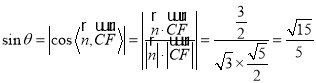 ,
,
![]() ,
,
即![]() 與平面
與平面![]() 所成角為
所成角為![]() .
.


科目:高中數學 來源: 題型:
【題目】某網絡營銷部門為了統計某市網友某日在某淘寶店的網購情況,隨機抽查了該市當天![]() 名網友的網購金額情況,得到如下統計表(如圖).
名網友的網購金額情況,得到如下統計表(如圖).
網購金額(單位:千元) | 頻數 | 頻率 |
| 3 | 0.05 |
|
|
|
| 9 | 0.15 |
| 15 | 0.25 |
| 18 | 0.30 |
|
|
|

若網購金額超過![]() 千元的顧客定義為“網購達人”,網購金額不超過
千元的顧客定義為“網購達人”,網購金額不超過![]() 千元的顧客定義為“非網購達人”,已知“非網購達人”與“網購達人”人數比恰好為
千元的顧客定義為“非網購達人”,已知“非網購達人”與“網購達人”人數比恰好為![]() .
.
(Ⅰ)試確定![]() 的值,并補全頻率分布直方圖(如圖);
的值,并補全頻率分布直方圖(如圖);
(Ⅱ)該營銷部門為了進一步了解這![]() 名網友的購物體驗,從“非網購達人”與“網購達人”中用分層抽樣的方法抽取
名網友的購物體驗,從“非網購達人”與“網購達人”中用分層抽樣的方法抽取![]() 人,若需從這
人,若需從這![]() 人中隨機選取
人中隨機選取![]() 人進行問卷調查.設
人進行問卷調查.設![]() 為選取的
為選取的![]() 人中“網購達人”的人數,求
人中“網購達人”的人數,求![]() 的分布列及其數學期望.
的分布列及其數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某機器生產商,對一次性購買兩臺機器的客戶推出兩種超過質保期后兩年內的延保維修方案:
方案一:交納延保金![]() 元,在延保的兩年內可免費維修
元,在延保的兩年內可免費維修![]() 次,超過
次,超過![]() 次每次收取維修費
次每次收取維修費![]() 元;
元;
方案二:交納延保金![]() 元,在延保的兩年內可免費維修
元,在延保的兩年內可免費維修![]() 次,超過
次,超過![]() 次每次收取維修費
次每次收取維修費![]() 元.
元.
某工廠準備一次性購買兩臺這種機器,現需決策在購買機器時應購買哪種延保方案,為此搜集并整理了臺這種機器超過質保期后延保兩年內維修的次數,統計得下表:
維修次數 | 0 | 1 | 2 | 3 |
機器臺數 | 20 | 10 | 40 | 30 |
以上![]() 臺機器維修次數的頻率代替一臺機器維修次數發生的概率,記
臺機器維修次數的頻率代替一臺機器維修次數發生的概率,記![]() 表示這兩臺機器超過質保期后延保兩年內共需維修的次數.
表示這兩臺機器超過質保期后延保兩年內共需維修的次數.
![]() 求
求![]() 的分布列;
的分布列;
![]() 以所需延保金與維修費用之和的期望值為決策依據,該工廠選擇哪種延保方案更合算?
以所需延保金與維修費用之和的期望值為決策依據,該工廠選擇哪種延保方案更合算?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 中,邊
中,邊![]() ,
,![]() ,令
,令![]() ,
,![]() ,
,![]() ,過
,過![]() 邊上一點
邊上一點![]() (異于端點)引邊
(異于端點)引邊![]() 的垂線
的垂線![]() ,垂足為
,垂足為![]() ,再由
,再由![]() 引邊
引邊![]() 的垂線
的垂線![]() ,垂足為
,垂足為![]() ,又由
,又由![]() 引邊
引邊![]() 的垂線
的垂線![]() ,垂足為
,垂足為![]() ,同樣的操作連續進行,得到點列
,同樣的操作連續進行,得到點列![]() 、
、![]() 、
、![]() ,設
,設![]() (
(![]() );
);
(1)求![]() ;
;
(2)結論“![]() ”是否正確?請說明理由;
”是否正確?請說明理由;
(3)若對于任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數學 來源: 題型:
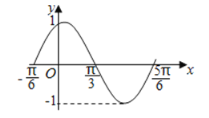
【題目】如圖是函數![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )在區間
)在區間![]() 上的圖象,為了得到這個函數的圖象,只需將
上的圖象,為了得到這個函數的圖象,只需將![]() (
(![]() )的圖象上的所有的點( )
)的圖象上的所有的點( )
A. 向左平移![]() 個長度單位,再把所得各點的橫坐標變為原來的
個長度單位,再把所得各點的橫坐標變為原來的![]() ,縱坐標不變
,縱坐標不變
B. 向左平移![]() 個長度單位,再把所得各點的橫坐標變為原來的2倍,縱坐標不變
個長度單位,再把所得各點的橫坐標變為原來的2倍,縱坐標不變
C. 向左平移![]() 個長度單位,再把所得各點的橫坐標變為原來的
個長度單位,再把所得各點的橫坐標變為原來的![]() ,縱坐標不變
,縱坐標不變
D. 向左平移![]() 個長度單位,再把所得各點的橫坐標變為原來的2倍,縱坐標不變
個長度單位,再把所得各點的橫坐標變為原來的2倍,縱坐標不變
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某部門經統計,客戶對不同款型理財產品的最滿意程度百分比和對應的理財總銷售量(萬元)如下表(最滿意度百分比超高時總銷售量最高):
產品款型 | A | B | C | D | E | F | G | H | I | J |
最滿意度% | 20 | 34 | 25 | 19 | 26 | 20 | 19 | 24 | 19 | 13 |
總銷量(萬元) | 80 | 89 | 89 | 78 | 75 | 71 | 65 | 62 | 60 | 52 |
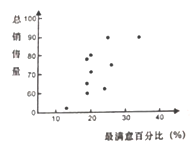
設![]() 表示理財產品最滿意度的百分比,
表示理財產品最滿意度的百分比,![]() 為該理財產品的總銷售量(萬元).這些數據的散點圖如圖所示.
為該理財產品的總銷售量(萬元).這些數據的散點圖如圖所示.
(1)在![]() 份
份![]() 款型理財產品的顧客滿意度調查資料中任取
款型理財產品的顧客滿意度調查資料中任取![]() 份;只有一份最滿意的,求含有最滿意客戶資料事件的概率.
份;只有一份最滿意的,求含有最滿意客戶資料事件的概率.
(2)我們約定:相關系數的絕對值在![]() 以下是無線性相關,在
以下是無線性相關,在![]() 以上(含
以上(含![]() )至
)至![]() 是一般線性相關,在
是一般線性相關,在![]() 以上(含
以上(含![]() )是較強線性相關,若沒有達到較強線性相關則采取“末位”剔除制度(即總銷售量最少的那一款產品退出理財銷售);試求在剔除“末位”款型后的線性回歸方程(系數精確到
)是較強線性相關,若沒有達到較強線性相關則采取“末位”剔除制度(即總銷售量最少的那一款產品退出理財銷售);試求在剔除“末位”款型后的線性回歸方程(系數精確到![]() ).
).
數據參考計算值:
項目 |
|
|
|
|
|
|
值 | 21.9 | 72.1 | 288.9 | 37.16 | 452.1 | 17.00 |
附:回歸直線方程![]() 的斜率和截距的最小二乘法估計分別為:
的斜率和截距的最小二乘法估計分別為:
線性相關系數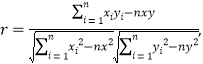
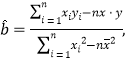
![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com