
【題目】四棱錐P﹣ABCD中,底面ABCD是邊長為2的菱形,側面PAD⊥底面ABCD,∠BCD=60°,PA=PD= ![]() ,E是BC中點,點Q在側棱PC上.
,E是BC中點,點Q在側棱PC上. 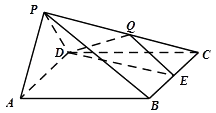
(1)求證:AD⊥PB;
(2)若Q是PC中點,求二面角E﹣DQ﹣C的余弦值;
(3)若 ![]() ,當PA∥平面DEQ時,求λ的值.
,當PA∥平面DEQ時,求λ的值.
【答案】
(1)證明:取AD中點O,連接OP,OB,BD.
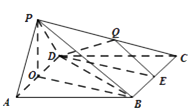
因為PA=PD,所以PO⊥AD.
因為菱形ABCD中,∠BCD=60°,所以AB=BD,所以BO⊥AD.
因為BO∩PO=O,所以AD⊥平面POB,所以AD⊥PB.
(2)解:由(1)知BO⊥AD,PO⊥AD.
因為側面PAD⊥底面ABCD,且平面PAD∩底面ABCD=AD,所以PO⊥底面ABCD.
以O為坐標原點,如圖建立空間直角坐標系O﹣xyz.
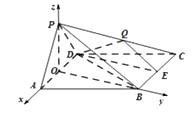
則D(﹣1,0,0), ![]() ,P(0,0,1),
,P(0,0,1), ![]() ,
,
因為Q為PC中點,所以 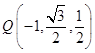 .
.
所以 ![]() ,
, 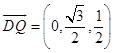 ,所以平面DEQ的法向量為
,所以平面DEQ的法向量為 ![]() .
.
因為 ![]() ,
, 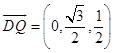 ,
,
設平面DQC的法向量為 ![]() ,則
,則  ,∴
,∴ 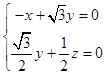
令 ![]() ,則y=1,
,則y=1, ![]() ,即
,即 ![]() .
. 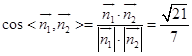 .
.
由圖可知,二面角E﹣DQ﹣C為銳角,所以余弦值為 ![]() .
.
(3)解:因為 ![]() ,所以
,所以 ![]() ,
,
由(2)知 ![]() ,
, ![]() ,
,
若設Q(x,y,z),則 ![]() ,
,
由 ![]() ,得
,得 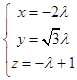 ,
,
在平面DEQ中, ![]() ,
, ![]() ,
,
所以平面DEQ法向量為 ![]() ,
,
又因為PA∥平面DEQ,所以 ![]() ,
,
即(1﹣λ)+(﹣1)(2λ﹣1)=0,得 ![]() .
.
所以,當 ![]() 時,PA∥平面DEQ.
時,PA∥平面DEQ.
【解析】(1)證明AD⊥平面POB,即可證明AD⊥PB;(2)證明PO⊥底面ABCD,建立空間直角坐標系,求出平面DEQ的法向量為 ![]() ,平面DQC的法向量
,平面DQC的法向量 ![]() ,利用向量的夾角公式,即可求得結論;(3)求出平面DEQ法向量為
,利用向量的夾角公式,即可求得結論;(3)求出平面DEQ法向量為 ![]() ,利用PA∥平面DEQ,即
,利用PA∥平面DEQ,即 ![]() ,從而可得結論.
,從而可得結論.
【考點精析】通過靈活運用直線與平面平行的判定和直線與平面垂直的性質,掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行;垂直于同一個平面的兩條直線平行即可以解答此題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】某電視傳媒公司為了了解某類體育節(jié)目的收視情況,隨機抽取了100名觀眾進行調查,如圖是根據(jù)調查結果繪制的觀眾日均收看該類體育節(jié)目時間的頻率分布直方圖,其中收看時間分組區(qū)間是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].將日均收看該類體育節(jié)目時間不低于40分鐘的觀眾稱為“體育迷”.則抽取的100名觀眾中“體育迷”有名. 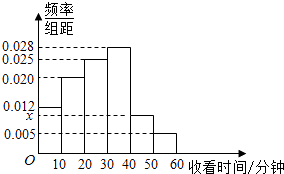
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(本題滿分16分)已知函數(shù)![]() ,
, ![]() .
.
(1)若函數(shù)![]() 在
在![]() 上單調遞增,求實數(shù)
上單調遞增,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若直線![]() 是函數(shù)
是函數(shù)![]() 圖象的切線,求
圖象的切線,求![]() 的最小值;
的最小值;
(3)當![]() 時,若
時,若![]() 與
與![]() 的圖象有兩個交點
的圖象有兩個交點![]() ,求證:
,求證: ![]()
![]() .(取
.(取![]() 為
為![]() ,取
,取![]() 為
為![]() ,取
,取![]() 為
為![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=ax3+bx+c在點x=2處取得極值c﹣16. (Ⅰ)求a,b的值;
(Ⅱ)若f(x)有極大值28,求f(x)在[﹣3,3]上的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
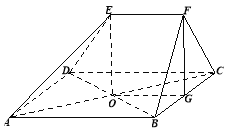
【題目】(本題滿分14分)
如圖,在多面體![]() 中,四邊形
中,四邊形![]() 是菱形,
是菱形,![]() 相交于點
相交于點![]() ,
,![]() ,
,![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() ,點
,點![]() 為
為![]() 的中點.
的中點.
(1)求證:直線![]() 平面
平面![]() ;
;
(2)求證:直線![]()
![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設對于任意實數(shù)x,不等式|x+7|+|x﹣1|≥m恒成立.
(1)求m的取值范圍;
(2)當m取最大值時,解關于x的不等式:|x﹣3|﹣2x≤2m﹣12.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某市政府為了實施政府績效管理、創(chuàng)新政府公共服務模式、提高公共服務效率.實施了“政府承諾,等你打分”民意調查活動,通過問卷調查了學生、在職人員、退休人員共250人,統(tǒng)計結果表不幸被污損,如表:
學生 | 在職人員 | 退休人員 | |
滿意 |
|
| 78 |
不滿意 | 5 |
| 12 |
若在所調查人員中隨機抽取1人,恰好抽到學生的概率為0.32.
(1)求滿意學生的人數(shù);
(2)現(xiàn)用分層抽樣的方法在所調查的人員中抽取25人,則在職人員應抽取多少人?
(3)若滿意的在職人員為77,則從問卷調查中填寫不滿意的“學生和在職人員”中選出2人進行訪談,求這2人中包含了兩類人員的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 。
。
(1)若f(x)的圖象與g(x)的圖象所在兩條曲線的一個公共點在y軸上,且在該點處兩條曲線的切線互相垂直,求b和c的值。
(2)若a=c=1,b=0,試比較f(x)與g(x)的大小,并說明理由;
(3)若b=c=0,證明:對任意給定的正數(shù)a,總存在正數(shù)m,使得當x![]() 時,
時,
恒有f(x)>g(x)成立。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列{an}的前n項和為Sn , 點(n, ![]() )在直線y=
)在直線y= ![]() x+
x+ ![]() 上. (Ⅰ)求數(shù)列{an}的通項公式;
上. (Ⅰ)求數(shù)列{an}的通項公式;
(Ⅱ)設bn= ![]() ,求數(shù)列{bn}的前n項和為Tn , 并求使不等式Tn>
,求數(shù)列{bn}的前n項和為Tn , 并求使不等式Tn> ![]() 對一切n∈N*都成立的最大正整數(shù)k的值.
對一切n∈N*都成立的最大正整數(shù)k的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com