
【題目】已知函數![]() ,
,
(1)求函數![]() 的單調區間;
的單調區間;
(2)若關于![]() 的方程
的方程![]() 有實數解,求實數
有實數解,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2) ![]() .
.
【解析】
(1)先利用導數研究![]() 時單調區間,再根據函數奇偶性確定
時單調區間,再根據函數奇偶性確定![]() 時單調區間,(2)先分離變量,轉化研究對應函數值域,再利用導數研究
時單調區間,(2)先分離變量,轉化研究對應函數值域,再利用導數研究![]() 時單調區間,根據函數奇偶性確定
時單調區間,根據函數奇偶性確定![]() 時單調區間,最后根據單調性確定函數值域,即得結果.
時單調區間,最后根據單調性確定函數值域,即得結果.
(1)函數![]() 的定義域為
的定義域為![]() 且
且![]() 關于坐標原點對稱,
關于坐標原點對稱,
![]() ,∴
,∴![]() 為偶函數,
為偶函數,
當![]() 時,
時,![]() ,
,
令![]()
![]()
![]() ,
,
令![]()
![]()
![]()
![]() .
.
所以可知:當![]() 時,
時,![]() 單調遞減,
單調遞減,
當![]() 時,
時,![]() 單調遞增,
單調遞增,
又因為![]() 是偶函數,所以在對稱區間上單調性相反,所以可得:
是偶函數,所以在對稱區間上單調性相反,所以可得:
當![]() 時,
時,![]() 單調遞增,
單調遞增,
當![]() 時,
時,![]() 單調遞減,
單調遞減,
綜上可得:![]() 的遞增區間是:
的遞增區間是:![]() ,
,![]() ;
;
![]() 的遞減區間是:
的遞減區間是:![]() ,
,![]() .
.
(2)由![]() ,即
,即![]() ,顯然,
,顯然,![]() ,
,
可得:![]() ,令
,令![]() ,
,
當![]() 時,
時,![]() ,
,
![]()
![]()
![]() .
.
顯然![]() ,當
,當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
∴![]() 時,
時,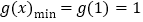 .
.
又![]() ,所以可得
,所以可得![]() 為奇函數,所以
為奇函數,所以![]() 圖像關于坐標原點對稱,
圖像關于坐標原點對稱,
所以可得:當![]() 時,
時,![]() ,
,
∴![]() 的值域為
的值域為![]() ,∴
,∴![]() 的取值范圍是
的取值范圍是![]() .
.


 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:高中數學 來源: 題型:
【題目】設函數f(x)= ![]() ﹣k(
﹣k( ![]() +lnx)(k為常數,e=2.71828…是自然對數的底數).
+lnx)(k為常數,e=2.71828…是自然對數的底數).
(1)當k≤0時,求函數f(x)的單調區間;
(2)若函數f(x)在(0,2)內存在兩個極值點,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知首項是1的兩個數列{an},{bn}(bn≠0,n∈N*)滿足anbn+1﹣an+1bn+2bn+1bn=0.
(1)令cn= ![]() ,求數列{cn}的通項公式;
,求數列{cn}的通項公式;
(2)若bn=3n﹣1 , 求數列{an}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,D,E,F分別為棱PC,AC,AB的中點,已知PA⊥AC,PA=6,BC=8,DF=5.求證: 
(1)直線PA∥平面DEF;
(2)平面BDE⊥平面ABC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex+e﹣x , 其中e是自然對數的底數.
(1)證明:f(x)是R上的偶函數;
(2)若關于x的不等式mf(x)≤e﹣x+m﹣1在(0,+∞)上恒成立,求實數m的取值范圍;
(3)已知正數a滿足:存在x0∈[1,+∞),使得f(x0)<a(﹣x03+3x0)成立,試比較ea﹣1與ae﹣1的大小,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,O為坐標原點,橢圓C1: ![]() +
+ ![]() =1(a>b>0)的左、右焦點分別為F1 , F2 , 離心率為e1;雙曲線C2:
=1(a>b>0)的左、右焦點分別為F1 , F2 , 離心率為e1;雙曲線C2: ![]() ﹣
﹣ ![]() =1的左、右焦點分別為F3 , F4 , 離心率為e2 , 已知e1e2=
=1的左、右焦點分別為F3 , F4 , 離心率為e2 , 已知e1e2= ![]() ,且|F2F4|=
,且|F2F4|= ![]() ﹣1.
﹣1. 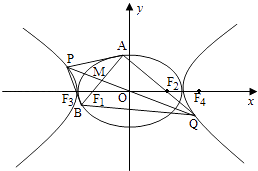
(1)求C1、C2的方程;
(2)過F1作C1的不垂直于y軸的弦AB,M為AB的中點,當直線OM與C2交于P,Q兩點時,求四邊形APBQ面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】計劃在某水庫建一座至多安裝3臺發電機的水電站,過去50年的水文資料顯示,水庫年入流量X(年入流量:一年內上游來水與庫區降水之和.單位:億立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超過120的年份有35年,超過120的年份有5年,將年入流量在以上三段的頻率作為相應段的概率,假設各年的年入流量相互獨立.
(1)求未來4年中,至多有1年的年入流量超過120的概率;
(2)水電站希望安裝的發電機盡可能運行,但每年發電機最多可運行臺數受年入流量X限制,并有如下關系:
年入流量X | 40<X<80 | 80≤X≤120 | X>120 |
發電機最多可運行臺數 | 1 | 2 | 3 |
若某臺發電機運行,則該臺年利潤為5000萬元,若某臺發電機未運行,則該臺年虧損800萬元,欲使水電站年總利潤的均值達到最大,應安裝發電機多少臺?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com