
【題目】已知函數![]() .
.
(1)當![]() 時,如果函數
時,如果函數![]() 僅有一個零點,求實數
僅有一個零點,求實數![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,試比較
時,試比較![]() 與1的大小;
與1的大小;
(3)求證:![]()
![]()
【答案】(1)![]() 的取值范圍是
的取值范圍是![]() 或
或![]() ;(2)①當
;(2)①當![]() 時,
時,![]() ,即
,即![]() ;
;
②當![]() 時,
時,![]() ,即
,即![]() ;③當
;③當![]() 時,
時,![]() ,即
,即![]() ;(3)證明過程詳見解析.
;(3)證明過程詳見解析.
【解析】試題分析:本題考查函數與導數、導數的運算、利用導數判斷函數的單調性、利用導數求函數的極值與最值等數學知識和方法,考查綜合運用數學知識和方法分析問題和解決問題的能力,考查函數思想和分類討論思想.第一問,先將![]() 代入得到
代入得到![]() 解析式,因為
解析式,因為![]() 僅有一個零點,所以
僅有一個零點,所以![]() 和
和![]() 僅有一個交點,所以關鍵是
僅有一個交點,所以關鍵是![]() 的圖像,對
的圖像,對![]() 求導,令
求導,令![]() 和
和![]() 判斷函數的單調性,確定函數的極值和最值所在位置,求出具體的數值,便可以描繪出函數圖像,來決定
判斷函數的單調性,確定函數的極值和最值所在位置,求出具體的數值,便可以描繪出函數圖像,來決定![]() 的位置;第二問,先將
的位置;第二問,先將![]() 代入,得到
代入,得到![]() 解析式,作差法比較大小,得到新函數
解析式,作差法比較大小,得到新函數![]() ,判斷
,判斷![]() 的正負即可,通過對
的正負即可,通過對![]() 求導,可以看出
求導,可以看出![]() 在
在![]() 上是增函數且
上是增函數且![]() ,所以分情況會出現3種大小關系;第三問,法一:利用第二問的結論,得到表達式
,所以分情況會出現3種大小關系;第三問,法一:利用第二問的結論,得到表達式![]() ,再利用不等式的性質得到所證表達式的右邊,左邊是利用對數的運算性質化簡,得證;法二,用數學歸納法證明,先證明當
,再利用不等式的性質得到所證表達式的右邊,左邊是利用對數的運算性質化簡,得證;法二,用數學歸納法證明,先證明當![]() 時不等式成立,再假設當
時不等式成立,再假設當![]() 時不等式成立,然后利用假設的結論證明當
時不等式成立,然后利用假設的結論證明當![]() 時不等式成立即可.
時不等式成立即可.
試題解析:(1)當![]() 時,
時,![]() ,定義域是
,定義域是![]() ,
,
![]() ,令
,令![]() ,得
,得![]() 或
或![]() .
.
∵當![]() 或
或![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
∴![]() 的極大值是
的極大值是![]() ,極小值是
,極小值是![]() .
.
∵當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
![]() 當
當![]() 僅有一個零點時,
僅有一個零點時,![]() 的取值范圍是
的取值范圍是![]() 或
或![]() . 4分
. 4分
(2)當![]() 時,
時,![]() ,定義域為
,定義域為![]() .
.
令![]() ,
,
![]() ,
,
![]() 在
在![]() 上是增函數.
上是增函數.
①當![]() 時,
時,![]() ,即
,即![]() ;
;
②當![]() 時,
時,![]() ,即
,即![]() ;
;
③當![]() 時,
時,![]() ,即
,即![]() . 8分
. 8分
(3)(法一)根據(2)的結論,當![]() 時,
時,![]() ,即
,即![]() .
.
令![]() ,則有
,則有![]() ,
,
![]() .
.![]() ,
,
![]() . 12分
. 12分
(法二)當![]() 時,
時,![]() .
.
![]() ,
,![]() ,即
,即![]() 時命題成立.
時命題成立.
設當![]() 時,命題成立,即
時,命題成立,即![]() .
.
![]() 時,
時,![]()
![]() .
.
根據(2)的結論,當![]() 時,
時,![]() ,即
,即![]() .
.
令![]() ,則有
,則有![]() ,
,
則有![]() ,即
,即![]() 時命題也成立.
時命題也成立.
因此,由數學歸納法可知不等式成立.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數學 來源: 題型:
【題目】袋中裝有黑球和白球共7個,從中任取2個球都是白球的概率為![]() .現在甲、乙兩人從袋中輪流摸取1球,甲先取,乙后取,然后甲再取…取后不放回,直到兩人中有一人取到白球時即終止,每個球在每一次被取出的機會是等可能的.
.現在甲、乙兩人從袋中輪流摸取1球,甲先取,乙后取,然后甲再取…取后不放回,直到兩人中有一人取到白球時即終止,每個球在每一次被取出的機會是等可能的.
(1)求袋中原有白球的個數;
(2)求取球兩次終止的概率
(3)求甲取到白球的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家庭記錄了未使用節水龍頭50天的日用水量數據(單位:m3)和使用了節水龍頭50天的日用水量數據,得到頻數分布表如下:
未使用節水龍頭50天的日用水量頻數分布表
日用 水量 |
|
|
|
|
|
|
|
頻數 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了節水龍頭50天的日用水量頻數分布表
日用 水量 |
|
|
|
|
|
|
頻數 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答題卡上作出使用了節水龍頭50天的日用水量數據的頻率分布直方圖:
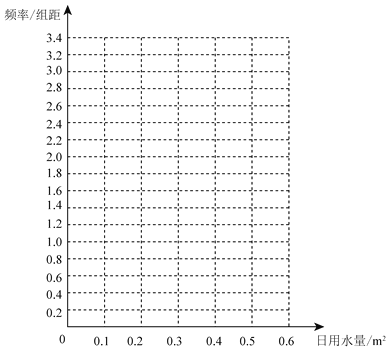
(2)估計該家庭使用節水龍頭后,日用水量小于0.35 m3的概率;
(3)估計該家庭使用節水龍頭后,一年能節省多少水?(一年按365天計算,同一組中的數據以這組數據所在區間中點的值作代表.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系.已知點
軸的正半軸為極軸建立極坐標系.已知點![]() 的直角坐標為
的直角坐標為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 過點
過點![]() 且與曲線
且與曲線![]() 相交于
相交于![]() ,
,![]() 兩點.
兩點.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() ,求直線
,求直線![]() 的直角坐標方程.
的直角坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國南宋數學家楊輝1261年所著的《詳解九章算法》一書里出現了如圖所示的表,即楊輝三角,這是數學史上的一個偉大成就.在“楊輝三角”中,已知第![]() 行的所有數字之和為
行的所有數字之和為![]() ,若去除所有為1的項,依次構成數列2,3,3,4,6,4,5,10,10,5,……,則此數列的前56項和為( )
,若去除所有為1的項,依次構成數列2,3,3,4,6,4,5,10,10,5,……,則此數列的前56項和為( )

A. 2060B. 2038C. 4084D. 4108
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知拋物線x2=2py(p>0)上的點M(m,1)到焦點F的距離為2, 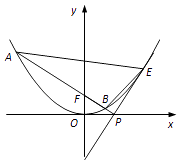
(1)求拋物線的方程;
(2)如圖,點E是拋物線上異于原點的點,拋物線在點E處的切線與x軸相交于點P,直線PF與拋物線相交于A,B兩點,求△EAB面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小陳同學進行三次定點投籃測試,已知第一次投籃命中的概率為![]() ,第二次投籃命中的概率為
,第二次投籃命中的概率為![]() ,前兩次投籃是否命中相互之間沒有影響.第三次投籃受到前兩次結果的影響,如果前兩次投籃至少命中一次,則第三次投籃命中的概率為
,前兩次投籃是否命中相互之間沒有影響.第三次投籃受到前兩次結果的影響,如果前兩次投籃至少命中一次,則第三次投籃命中的概率為![]() ,否則為
,否則為![]() .
.
(1)求小陳同學三次投籃至少命中一次的概率;
(2)記小陳同學三次投籃命中的次數為隨機變量![]() ,求
,求![]() 的概率分布及數學期望.
的概率分布及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某學校高三年級共800名男生中隨機抽取50人測量身高.據測量,被測學生身高全部介于![]() 到
到![]() 之間,將測量結果按如下方式分成八組:第一組
之間,將測量結果按如下方式分成八組:第一組![]() ;第二組
;第二組![]() ;…;第八組
;…;第八組![]() .如圖是按上述分組方法得到的頻率分布直方圖的一部分.已知第一組與第八組人數相同,第六組、第七組、第八組人數依次構成等差數列.
.如圖是按上述分組方法得到的頻率分布直方圖的一部分.已知第一組與第八組人數相同,第六組、第七組、第八組人數依次構成等差數列.

(1)估計這所學校高三年級全體男生身高在![]() 以上(含
以上(含![]() )的人數;
)的人數;
(2)求第六組、第七組的頻率并補充完整頻率分布直方圖;
(3)若從身高屬于第六組和第八組的所有男生中隨機抽取兩人,記他們的身高分別為![]() ,求滿足“
,求滿足“![]() ”的事件的概率.
”的事件的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com