Question

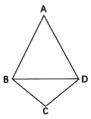
【題目】如圖，四邊形，，，現將沿折起，當二面角的大小在時，直線和所成角為，則的最大值為（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】

取BD中點O，連結AO，CO，以O為原點，OC為x軸，OD為y軸，過點O作平面BCD的垂線為z軸，建立空間直角坐標系，利用向量法能求出直線AB與CD所成角的余弦值取值范圍．

解：取BD中點O，連結AO，CO，

∵AB＝BD＝DA＝4．BC＝CD，∴CO⊥BD，AO⊥BD，且CO＝2，AO，

∴∠AOC是二面角A﹣BD﹣C的平面角，

以O為原點，OC為x軸，OD為y軸，

過點O作平面BCD的垂線為z軸，建立空間直角坐標系，

B（0，﹣2，0），C（2，0，0），D（0，2，0），

設二面角A﹣BD﹣C的平面角為θ，則，

連AO、BO，則∠AOC＝θ，A（），

∴，，

設AB、CD的夾角為α，

則cosα，

∵，∴cos，∴|1|∈[0，1+]．

∴cos的最大值為．

故選：C．