
【題目】如圖,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的右焦點為
的右焦點為![]() ,下頂點為P,過點
,下頂點為P,過點![]() 的動直線l交橢圓C于A,B兩點.
的動直線l交橢圓C于A,B兩點.
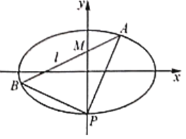
(1)當直線l平行于x軸時,P,F,A三點共線,且![]() ,求橢圓C的方程;
,求橢圓C的方程;
(2)當橢圓C的離心率為何值時,對任意的動直線l,總有![]() ?
?
【答案】(1)![]() (2)橢圓C的離心率為
(2)橢圓C的離心率為![]()
【解析】
(1)當直線![]() 與x軸平行,由
與x軸平行,由![]() ,得到
,得到![]() 點坐標,根據
點坐標,根據![]() ,得到
,得到![]() 的值,將
的值,將![]() 點代入橢圓方程,得到
點代入橢圓方程,得到![]() 和
和![]() ,從而得到所求橢圓方程;
,從而得到所求橢圓方程;
(2)①當直線l平行于x軸時,由![]() ,得到
,得到![]() ,從而得到
,從而得到![]() ,根據
,根據![]() 得到
得到![]() ,從而得到離心率
,從而得到離心率![]() ,②當直線l不平行于x軸時,當
,②當直線l不平行于x軸時,當![]() ,橢圓方程轉化為
,橢圓方程轉化為![]() ,將直線l:
,將直線l:![]() 與橢圓聯立,得到
與橢圓聯立,得到![]() ,
,![]() ,再對
,再對![]() 進行化簡,可得
進行化簡,可得![]() ,從而得到所求橢圓離心率為
,從而得到所求橢圓離心率為![]() .
.
解:(1)當直線![]() 與x軸平行時,即
與x軸平行時,即![]() ,
,
如圖,作![]() 軸于點D,
軸于點D,
則根據![]() ,可得
,可得![]() ,
,
且![]() ,
,
解得![]() ,
,
又因為![]() 在橢圓上,所以
在橢圓上,所以 ,
,
解得![]()
所以![]() ,
,
所以橢圓C的方程為![]() ;
;

(2)①當直線l平行于x軸時,
由![]() ,得
,得
∴![]() ,又
,又![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() .
.
②當直線l不平行于x軸時,下面證明當![]() ,總有
,總有![]() ,
,
事實上,由①知橢圓可化為![]() ,
,
∴![]() ,
,
直線l的方程為![]() ,
,![]() ,
,![]() ,
,
由 ,得
,得![]() ,
,
∴![]() ,
,
∵![]() ,
,![]()
∴![]()
![]()
![]()

 .
.
∴![]() ,
,
綜上,當橢圓C的離心率為![]() 時,對任意的動直線l,總有
時,對任意的動直線l,總有![]() .
.


科目:高中數學 來源: 題型:
【題目】點![]() 是拋物線
是拋物線![]() 內一點,
內一點,![]() 是拋物線
是拋物線![]() 的焦點,
的焦點,![]() 是拋物線
是拋物線![]() 上任意一點,且已知
上任意一點,且已知![]() 的最小值為2.
的最小值為2.
(1)求拋物線![]() 的方程;
的方程;
(2)拋物線![]() 上一點
上一點![]() 處的切線與斜率為常數
處的切線與斜率為常數![]() 的動直線
的動直線![]() 相交于
相交于![]() ,且直線
,且直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() 、
、![]() 兩點.問是否有常數
兩點.問是否有常數![]() 使
使![]() ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著網購人數的日益增多,網上的支付方式也呈現一種多樣化的狀態,越來越多的便捷移動支付方式受到了人們的青睞,更被網友們評為“新四大發明”之一.隨著人們消費觀念的進步,許多人喜歡用信用卡購物,考慮到這一點,一種“網上的信用卡”橫空出世——螞蟻花唄.這是一款支付寶和螞蟻金融合作開發的新支付方式,簡單便捷,同時也滿足了部分網上消費群體在支付寶余額不足時的“賒購”消費需求.為了調查使用螞蟻花唄“賒購”消費與消費者年齡段的關系,某網站對其注冊用戶開展抽樣調查,在每個年齡段的注冊用戶中各隨機抽取100人,得到各年齡段使用螞蟻花唄“賒購”的人數百分比如圖所示.
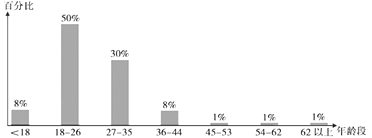
(1)由大數據可知,在18到44歲之間使用花唄“賒購”的人數百分比y與年齡x成線性相關關系,利用統計圖表中的數據,以各年齡段的區間中點代表該年齡段的年齡,求所調查群體各年齡段“賒購”人數百分比y與年齡x的線性回歸方程(回歸直線方程的斜率和截距保留兩位有效數字);
(2)該網站年齡為20歲的注冊用戶共有2000人,試估算該網站20歲的注冊用戶中使用花唄“賒購”的人數;
(3)已知該網店中年齡段在18-26歲和27-35歲的注冊用戶人數相同,現從18到35歲之間使用花唄“賒購”的人群中按分層抽樣的方法隨機抽取8人,再從這8人中簡單隨機抽取2人調查他們每個月使用花唄消費的額度,求抽取的兩人年齡都在18到26歲的概率.
參考答案: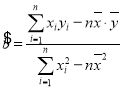 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,直角梯形![]() 中,
中,![]() ,
,![]() ,E、F分別是
,E、F分別是![]() 和
和![]() 上的點,且
上的點,且![]() ,
,![]() ,
,![]() ,沿
,沿![]() 將四邊形
將四邊形![]() 折起,如圖2,使
折起,如圖2,使![]() 與
與![]() 所成的角為60°.
所成的角為60°.
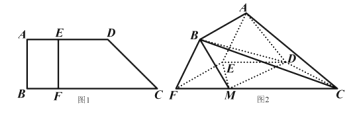
(1)求證:![]() 平面
平面![]() ;
;
(2)M為![]() 上的點,
上的點,![]() ,若二面角
,若二面角![]() 的余弦值為
的余弦值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為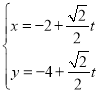 (t為參數),以坐標原點O為極點,以x軸的非負半軸為極軸,取相同的單位長度建立極坐標系,曲線C的極坐標方程為
(t為參數),以坐標原點O為極點,以x軸的非負半軸為極軸,取相同的單位長度建立極坐標系,曲線C的極坐標方程為![]() .
.
(1)寫出直線![]() 的普通方程和曲線C的直角坐標方程;
的普通方程和曲線C的直角坐標方程;
(2)已知定點![]() ,直線
,直線![]() 與曲線C分別交于P、Q兩點,求
與曲線C分別交于P、Q兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,已知曲線C1:x2+y2=1,以平面直角坐標系xoy的原點O為極點,x軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線![]() :ρ(2cosθ-sinθ)=6.
:ρ(2cosθ-sinθ)=6.
(Ⅰ)將曲線C1上的所有點的橫坐標,縱坐標分別伸長為原來的![]() 、2倍后得到曲線C2,試寫出直線
、2倍后得到曲線C2,試寫出直線![]() 的直角坐標方程和曲線C2的參數方程.
的直角坐標方程和曲線C2的參數方程.
(Ⅱ)在曲線C2上求一點P,使點P到直線l的距離最大,并求出此最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x-m|-|2x+2m|(m>0).
(Ⅰ)當m=1時,求不等式f(x)≥1的解集;
(Ⅱ)若x∈R,t∈R,使得f(x)+|t-1|<|t+1|,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com