【題目】某高校在2016年的自主招生考試成績中隨機抽取100名學生的筆試成績，按成績分組，得到的頻率分布表如下表所示．
組號 | 分組 | 頻數 | 頻率 |
第1組 |
| 5 | 0.050 |
第2組 |
| n | 0.350 |
第3組 |
| 30 | p |
第4組 |
| 20 | 0.200 |
第5組 |
| 10 | 0.100 |
合計 | 100 | 1.000 |
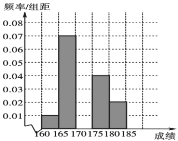
（1）求頻率分布表中n，p
（2）為了能選拔出最優秀的學生，高校決定在筆試成績高的第3、4、5組中用分層抽樣的方法抽取6名學生進入第二輪面試，則第3、4、5組每組各抽取多少名學生進入第二輪面試？
（3）在（2）的前提下，學校決定從6名學生中隨機抽取2名學生接受甲考官的面試，求第4組至少有1名學生被甲考官面試的概率．
【答案】（1）
，
，中位數估計值為171.7（2）第3、4、5組每組各抽學生人數為3、2、1（3）
【解析】
（1）由頻率分布表可得：，，由中位數的求法可得中位數估計值為171.7；
（2）因為筆試成績高的第3、4、5組的人數之比為
，由分層抽樣的方法選6名學生，三個小組分別選的人數為3、2、1；
（3）先列舉出從6名學生中隨機抽取2名學生的不同取法，再列舉出第4組至少有1名學生被甲考官面試的取法，再結合古典概型的概率公式即可得解.
解：（1）由已知：
，
，
，，中位數為
171.7，
即中位數估計值為171.7，
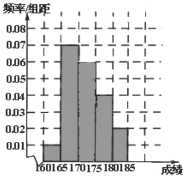
（2）由已知，筆試成績高的第3、4、5組的人數之比為，現用分層抽樣的方法選6名學生。故第3、4、5組每組各抽學生人數為3、2、1。
（3）在（2）的前提下，記第3組的3名學生為
，
，
，
第4組的2名學生為
，
，第5組的1名學生為
，且“第4組至少有1名學生被甲考官面試”為事件A。
則所有的基本事件有：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，一共15種。
A事件有：，，，，，，，，，一共9種。
，
答：第4組至少有1名學生被甲考官面試的概率為。
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】下列說法錯誤的是（ ）
A.命題“若
，則
”的逆否命題是“若
，則
”
B.“
”是“
”的充分不必要條件
C.若
為假命題，則
、
均為假命題
D.命題：“
，使得
”，則非：“
，
”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，以原點O為極點，x軸的正半軸為極軸建立極坐標系，已知直線l的參數方程為：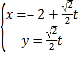
，
為參數
點的極坐標為
，曲線C的極坐標方程為
．
Ⅰ
試將曲線C的極坐標方程化為直角坐標方程，并求曲線C的焦點在直角坐標系下的坐標；
Ⅱ設直線l與曲線C相交于兩點A，B，點M為AB的中點，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}為等比數列，a1=2，公比q＞0，且a2，6，a3成等差數列．
（1）求數列{an}的通項公式；
（2）設bn=log2an，
，求使
的n的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在
中，已知
，
，
，D是邊AC上一點，將
沿BD折起，得到三棱錐
．若該三棱錐的頂點A在底面BCD的射影M在線段BC上，設
，則x的取值范圍為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為踐行“綠水青山就是金山銀山”的發展理念，某城區對轄區內
，
，
三類行業共200個單位的生態環境治理成效進行了考核評估，考評分數達到80分及其以上的單位被稱為“星級”環保單位，未達到80分的單位被稱為“非星級”環保單位．現通過分層抽樣的方法獲得了這三類行業的20個單位，其考評分數如下：
類行業：85，82，77，78，83，87；
類行業：76，67，80，85，79，81；
類行業：87，89，76，86，75，84，90，82．
（Ⅰ）計算該城區這三類行業中每類行業的單位個數；
（Ⅱ）若從抽取的類行業這6個單位中，再隨機選取3個單位進行某項調查，求選出的這3個單位中既有“星級”環保單位，又有“非星級”環保單位的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
