【題目】在“挑戰不可能”的電視節目上，甲、乙、丙三個人組成的解密團隊參加一項解密挑戰活動，規則是由密碼專家給出題目，然后由3個人依次出場解密，每人限定時間是1分鐘內，否則派下一個人.3個人中只要有一人解密正確，則認為該團隊挑戰成功，否則挑戰失敗.根據甲以往解密測試情況，抽取了甲100次的測試記錄，繪制了如圖所示的頻率分布直方圖.
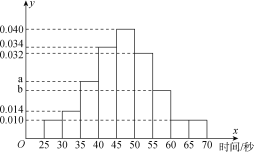
（1）若甲解密成功所需時間的中位數為47，求
、
的值，并求出甲在1分鐘內解密成功的頻率；
（2）在“挑戰不可能”節目上由于來自各方及自身的心理壓力，甲，乙，丙解密成功的概率分別為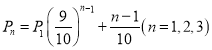
，其中
表示第
個出場選手解密成功的概率，并且
定義為甲抽樣中解密成功的頻率代替，各人是否解密成功相互獨立.
①求該團隊挑戰成功的概率；
②該團隊以從小到大的順序按排甲、乙、丙三個人上場解密，求團隊挑戰成功所需派出的人數
的可能值及其概率.
【答案】（1）
，
，0.9；（2）①
；②1，2，3；0.009.
【解析】
(1)根據中位數為47，則在頻率分布直方圖中時間位于47左邊的小長方形的面積之和為0.5，可求出
的值, 時間位于47右邊的小長方形的面積之和為0.5，可求出
的值.
(2) ①先分別求出三人解密成功的概率，然后先求出三人都沒有解密成功的概率，再求出團隊解密成功的概率.
②由①可知按
從小到大的順序的概率分別
，
，
，
的取值為1，2，3,在計算概率.
（1）甲解密成功所需時間的中位數為47，
，
解得；
，
解得；
甲在1分鐘內解密成功的頻率是
（2）①由題意及（1）可知第一個出場選手解密成功的概率為
；
第二個出場選手解密成功的概率為
，
第三個出場選手解密成功的概率為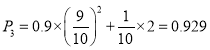
，
令“該團隊挑戰成功”的事件為
，“挑戰不成功”的事件為
，
，
該團隊挑戰成功的概率為
（或該團隊挑戰成功的概率為
）
②由①可知按從小到大的順序的概率分別
，
，
，
根據題意知的取值為1，2，3；
則
，
，
.
備戰中考寒假系列答案科目：高中數學 來源： 題型：
【題目】為配合“2019雙十二”促銷活動，某公司的四個商品派送點如圖環形分布，并且公司給
四個派送點準備某種商品各50個.根據平臺數據中心統計發現，需要將發送給四個派送點的商品數調整為40，45，54，61，但調整只能在相鄰派送點進行，每次調動可以調整1件商品.為完成調整，則（ ）
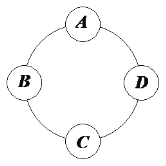
A.最少需要16次調動，有2種可行方案
B.最少需要15次調動，有1種可行方案
C.最少需要16次調動，有1種可行方案
D.最少需要15次調動，有2種可行方案
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某縣精準扶貧攻堅力公室決定派遣8名干部（5男3女）分成兩個小組，到該縣甲、乙兩個貧困村去參加扶貧工作，若要求每組至少3人，且每組均有男干部參加，則不同的派遣方案共有______種．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】圖，從甲地到丙地要經過兩個十字路口（十字路口
與十字路口
），從乙地到丙地也要經過兩個十字路口（十字路口
與十字路口
），設各路口信號燈工作相互獨立，且在，，，路口遇到紅燈的概率分別為
，，
，.
（1）求一輛車從乙地到丙地至少遇到一個紅燈的概率；
（2）若小方駕駛一輛車從甲地出發，小張駕駛一輛車從乙地出發，他們相約在丙地見面，記
表示這兩人見面之前車輛行駛路上遇到的紅燈的總個數，求的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，
的參數方程為
（t為參數）.以坐標原點O為極點，x軸的正半軸為極軸建立極坐標系，曲線C的極坐標方程為
.
（1）求的普通方程和曲線C的直角坐標方程；
（2）求曲線C上的點到距離的最大值及該點坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
