
【題目】命題p:實數x滿足![]() ,命題
,命題![]() :實數x滿足
:實數x滿足
(1)若![]() ,且
,且![]() 為真,求實數
為真,求實數![]() 的取值范圍;
的取值范圍;
(2)若![]()
![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
試題首先根據命題的要求,解出命題p和命題q所表示的含義,第一步a=1,解出一元二次不等式得出x的范圍,再解不等式組得出命題q所表示的x的范圍,由于p且q為真,說明p、q均為真,求出交集;第二步,q是非p的充分條件,先求出非p所表示的集合,根據q所表示的集合是非p所表示的集合的子集,求出實數a的范圍.
試題解析:
(1)由于a=1,則x2-4ax+3a2<0x2-4x+3<01<x<3.所以p:1<x<3,解不等式組 得2<x≤3,所以q:2<x≤3,由于p∧q為真,所以p,q均是真命題,解不等式組
得2<x≤3,所以q:2<x≤3,由于p∧q為真,所以p,q均是真命題,解不等式組![]() 得2<x<3,所以實數x的取值范圍是(2,3).
得2<x<3,所以實數x的取值范圍是(2,3).
(2)![]() :x2-4ax+3a2≥0,a>0,x2-4ax+3a2≥0(x-a)(x-3a)≥0x≤a或x≥3a,所以
:x2-4ax+3a2≥0,a>0,x2-4ax+3a2≥0(x-a)(x-3a)≥0x≤a或x≥3a,所以![]() :x≤a或x≥3a,設A={x|x≤a或x≥3a},由(1)知q:2<x≤3,設B={x|2<x≤3}.由于q
:x≤a或x≥3a,設A={x|x≤a或x≥3a},由(1)知q:2<x≤3,設B={x|2<x≤3}.由于q![]() ,所以
,所以![]() ,所以3≤a或3a≤2,即0<a≤
,所以3≤a或3a≤2,即0<a≤![]() 或a≥3,所以實數a的取值范圍是
或a≥3,所以實數a的取值范圍是![]() ∪[3,+∞).
∪[3,+∞).


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,圓
軸正半軸為極軸,建立極坐標系,圓![]() 的方程為
的方程為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(I )寫出![]() 的極坐標方程和
的極坐標方程和![]() 的平面直角坐標方程;
的平面直角坐標方程;
(Ⅱ) 若直線![]() 的極坐標方程為
的極坐標方程為![]() ,設
,設![]() 與
與![]() 的交點為
的交點為![]() 與
與![]() 的交點為
的交點為![]() 求
求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天氣預報說,在今后的三天中,每一天下雨的概率均為40%.現采用隨機模擬試驗的方法估計這三天中恰有兩天下雨的概率:先利用計算器產生0到9之間取整數值的隨機數,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三個隨機數作為一組,代表這三天的下雨情況.經隨機模擬試驗產生了如下20組隨機數:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
據此估計,這三天中恰有兩天下雨的概率近似為
A.0.35 B.0.25 C.0.20 D.0.15
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在平面直角坐標系中,直線![]() 的參數方程為
的參數方程為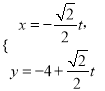 (其中t為參數),現以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為
(其中t為參數),現以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]() .
.
(1)寫出直線l普通方程和曲線C的直角坐標方程;
(2)過點![]() 且與直線
且與直線![]() 平行的直線
平行的直線![]() 交
交![]() 于
于![]() ,
, ![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某單位的食堂中,食堂每天以![]() 元/斤的價格購進米粉,然后以4.4元/碗的價格出售,每碗內含米粉0.2斤,如果當天賣不完,剩下的米粉以2元/斤的價格賣給養豬場.根據以往統計資料,得到食堂某天米粉需求量的頻率分布直方圖如圖所示,若食堂某天購進了80斤米粉,以
元/斤的價格購進米粉,然后以4.4元/碗的價格出售,每碗內含米粉0.2斤,如果當天賣不完,剩下的米粉以2元/斤的價格賣給養豬場.根據以往統計資料,得到食堂某天米粉需求量的頻率分布直方圖如圖所示,若食堂某天購進了80斤米粉,以![]() (單位:斤)(其中
(單位:斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (單位:元)表示利潤.
(單位:元)表示利潤.
(Ⅰ)計算當天米粉需求量的平均數,并直接寫出需求量的眾數和中位數;
(Ⅱ) 將![]() 表示為
表示為![]() 的函數;
的函數;
(Ⅲ)根據直方圖估計該天食堂利潤不少于760元的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}滿足當n>1時,an=![]() ,且a1=
,且a1=![]() .
.
(1)求證:數列![]() 為等差數列;
為等差數列;
(2)a1a2是否是數列{an}中的項?如果是,求出是第幾項;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象經過點(
的圖象經過點(![]() ,
,![]() )和(
)和(![]() ,
,![]() ),完成下面問題:
),完成下面問題:

(1)求函數![]() 的表達式;
的表達式;
(2)在給出的平面直角坐標系中,請用適當的方法畫出這個函數的圖象,并寫出這個函數的一條性質;
(3)已知函數![]() 的圖象如圖所示,結合你所畫出
的圖象如圖所示,結合你所畫出![]() 的圖象,直接寫出
的圖象,直接寫出![]() 的解集.
的解集.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業開發生產了一種大型電子產品,生產這種產品的年固定成本為2500萬元,每生產![]() 百件,需另投入成本
百件,需另投入成本![]() (單位:萬元),當年產量不足30百件時,
(單位:萬元),當年產量不足30百件時,![]() ;當年產量不小于30百件時,
;當年產量不小于30百件時,![]() ;若每件電子產品的售價為5萬元,通過市場分析,該企業生產的電子產品能全部銷售完.
;若每件電子產品的售價為5萬元,通過市場分析,該企業生產的電子產品能全部銷售完.
(1)求年利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (百件)的函數關系式;
(百件)的函數關系式;
(2)年產量為多少百件時,該企業在這一電子產品的生產中獲利最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com