
【題目】選修4-4:坐標系與參數方程
極坐標系中, ![]() 為極點,半徑為2的圓
為極點,半徑為2的圓![]() 的圓心坐標為
的圓心坐標為![]() .
.
(1)求圓![]() 的極坐標方程;
的極坐標方程;
(2)設直角坐標系的原點與極點![]() 重合,
重合, ![]() 軸非負關軸與極軸重合,直線
軸非負關軸與極軸重合,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),由直線
為參數),由直線![]() 上的點向圓
上的點向圓![]() 引切線,求切線長的最小值.
引切線,求切線長的最小值.
科目:高中數學 來源: 題型:
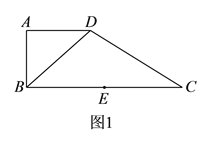
【題目】如圖![]() ,在直角梯形
,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,點
,點![]() 是
是![]() 邊的中點,將
邊的中點,將![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,連接
,連接![]() ,
, ![]() ,
, ![]() ,得到如圖
,得到如圖![]() 所示的幾何體.
所示的幾何體.
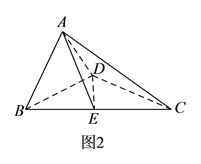
(Ⅰ)求證: ![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,
, ![]() 與其在平面
與其在平面![]() 內的正投影所成角的正切值為
內的正投影所成角的正切值為![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】田忌和齊王賽馬是歷史上有名的故事,設齊王的三匹馬分別為A、B、C,田忌的三匹馬分別為a、b、c.三匹馬各比賽一次,勝兩場者為獲勝.若這六匹馬比賽的優劣程度可以用以下不等式表示:A>a>B>b>C>c. (Ⅰ)如果雙方均不知道對方馬的出場順序,求田忌獲勝的概率;
(Ⅱ)為了得到更大的獲勝概率,田忌預先派出探子到齊王處打探實情,得知齊王第一場必出上等馬.那么,田忌應怎樣安排出馬的順序,才能使自己獲勝的概率最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}滿足a3=7,a5+a7=26,數列{an}的前n項和為Sn .
(Ⅰ)求an;
(Ⅱ)設bn= ![]() ,求數列{bn}的前n項和Tn .
,求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分16分)已知函數![]() 在
在![]() 處的切線方程為
處的切線方程為![]()
(1)若![]() =
= ![]() ,求證:曲線
,求證:曲線![]() 上的任意一點處的切線與直線
上的任意一點處的切線與直線![]() 和直線
和直線![]()
圍成的三角形面積為定值;
(2)若![]() ,是否存在實數
,是否存在實數![]() ,使得
,使得![]() 對于定義域內的任意
對于定義域內的任意![]() 都成立;
都成立;
(3)在(2)的條件下,若方程![]() 有三個解,求實數
有三個解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的頂點A(5,1),AB邊上的中線CM所在的直線方程為2x﹣y﹣5=0,AC邊上的高BH所在直線的方程為x﹣2y﹣5=0.
(1)求直線BC的方程;
(2)求直線BC關于CM的對稱直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b是正實數,設函數f(x)=xlnx,g(x)=﹣a+xlnb.
(Ⅰ)設h(x)=f(x)﹣g(x),求h(x)的單調區間;
(Ⅱ)若存在x0 , 使x0∈[ ![]() ,
, ![]() ]且f(x0)≤g(x0)成立,求
]且f(x0)≤g(x0)成立,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com