
設(shè)Sn是等差數(shù)列{an}的前n項(xiàng)和,已知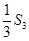 與
與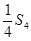 的等比中項(xiàng)為
的等比中項(xiàng)為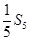 ,
,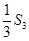 與
與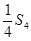 的等差中項(xiàng)為1,求等差數(shù)列{an}的通項(xiàng)。
的等差中項(xiàng)為1,求等差數(shù)列{an}的通項(xiàng)。
an=1或an=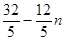
解析試題分析:利用等差數(shù)列的前n項(xiàng)和公式代入已知條件,建立d與a1的方程,聯(lián)立可求得數(shù)列的首項(xiàng)a1、公差d,再由等差數(shù)列的通項(xiàng)公式可求得an。解:設(shè)等差數(shù)列{an}的首項(xiàng)a1=a,公差為d,則通項(xiàng)為,an=a+(n-1)d,前n項(xiàng)和為Sn,代入已知關(guān)系式中,可知有由此得an=1;或an=4-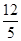 (n-1)=
(n-1)=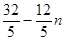 經(jīng)驗(yàn)證知時(shí)an=1,S5=5,或an=
經(jīng)驗(yàn)證知時(shí)an=1,S5=5,或an=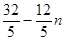 時(shí),S5=-4,均適合題意.故所求等差數(shù)列的通項(xiàng)為an=1,或an=
時(shí),S5=-4,均適合題意.故所求等差數(shù)列的通項(xiàng)為an=1,或an=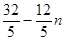
考點(diǎn):等差數(shù)列、等比數(shù)列
點(diǎn)評:本小題主要考查等差數(shù)列、等比數(shù)列、方程組等基礎(chǔ)知識,考查運(yùn)算能力.由等差數(shù)列的前n項(xiàng)和確定基本量 d與a1,之間的關(guān)系,關(guān)鍵在于熟練應(yīng)用公式


 期末100分闖關(guān)海淀考王系列答案
期末100分闖關(guān)海淀考王系列答案 小學(xué)能力測試卷系列答案
小學(xué)能力測試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知數(shù)列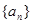 是等差數(shù)列,
是等差數(shù)列,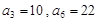 ,數(shù)列
,數(shù)列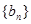 的前n項(xiàng)和是
的前n項(xiàng)和是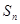 ,且
,且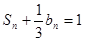 .
.
(I)求數(shù)列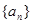 的通項(xiàng)公式;
的通項(xiàng)公式;
(II)求證:數(shù)列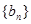 是等比數(shù)列;
是等比數(shù)列;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)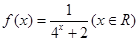 .
.
(1)求: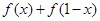 的值;
的值;
(2)類比等差數(shù)列的前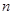 項(xiàng)和公式的推導(dǎo)方法,求:
項(xiàng)和公式的推導(dǎo)方法,求: 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在數(shù)列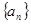 中,
中, ,
,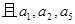 構(gòu)成公比不等于1的等比數(shù)列.
構(gòu)成公比不等于1的等比數(shù)列.
(1)求證數(shù)列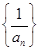 是等差數(shù)列;
是等差數(shù)列;
(2)求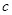 的值;
的值;
(3)數(shù)列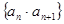 的前n項(xiàng)和為
的前n項(xiàng)和為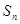 ,若對任意
,若對任意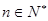 均有
均有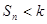 成立,求實(shí)數(shù)
成立,求實(shí)數(shù) 的范圍.
的范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
數(shù)列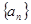 中,
中,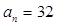 ,
, ,
,
(1)若 為公差為11的等差數(shù)列,求
為公差為11的等差數(shù)列,求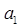 ;
;
(2)若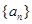 是以
是以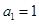 為首項(xiàng)、公比為
為首項(xiàng)、公比為 的等比數(shù)列,求
的等比數(shù)列,求 的值,并證明對任意
的值,并證明對任意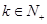 總有:
總有: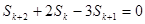
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
本小題滿分12分)設(shè)a、b、c成等比數(shù)列,非零實(shí)數(shù)x,y分別是a與b, b與c的等差中項(xiàng)。
(1)已知①a=1、b=2、c=4,試計(jì)算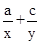 的值;
的值;
②a=-1、b= 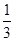 、c="-"
、c="-" 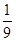 ,試計(jì)算
,試計(jì)算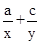 的值
的值
(2)試推測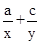 與2的大小關(guān)系,并證明你的結(jié)論。
與2的大小關(guān)系,并證明你的結(jié)論。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知等差數(shù)列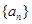 的前
的前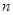 項(xiàng)和為
項(xiàng)和為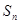 ,且
,且
(1)求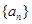 通項(xiàng)公式;
通項(xiàng)公式;
(2)求數(shù)列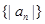 的前
的前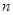 項(xiàng)和
項(xiàng)和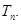
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知等差數(shù)列 的前四項(xiàng)和為10,且
的前四項(xiàng)和為10,且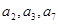 成等比數(shù)列
成等比數(shù)列
(1)求通項(xiàng)公式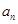
(2)設(shè)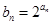 ,求數(shù)列
,求數(shù)列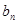 的前
的前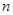 項(xiàng)和
項(xiàng)和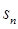 。
。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com