
【題目】下列敘述正確的是( )
A.命題“p且q”為真,則![]() 恰有一個為真命題
恰有一個為真命題
B.命題“已知![]() ,則“
,則“![]() ”是“
”是“![]() ”的充分不必要條件”
”的充分不必要條件”
C.命題![]() 都有
都有![]() ,則
,則![]() ,使得
,使得![]()
D.如果函數![]() 在區間
在區間![]() 上是連續不斷的一條曲線,并且有
上是連續不斷的一條曲線,并且有![]() ,那么函數
,那么函數![]() 在區間
在區間![]() 內有零點
內有零點
【答案】C
【解析】
由p且q的真值表,可判斷正誤;由充分必要條件的定義和特值法,可判斷正誤;由全稱命題的否定為特稱命題,可判斷正誤;由函數零點存在定理可判斷正誤.
解:對于A,命題“P且q為真,則P,q均為真命題”,故錯誤;
對于B,“a>b”推不出“a2>b2”,比如a=1,b=﹣1;反之也推不出,比如a=﹣2,b=0,“a>b”是“a2>b2”的不充分不必要條件,故錯誤;
對于C,命題![]() 都有
都有![]() ,則
,則![]() ,使得
,使得![]() ,故正確;
,故正確;
對于D,如果函數y=f(x)在區間[a,b]上是連續不斷的一條曲線,
并且有f(a)f(b)<0,由零點存在定理可得函數y=f(x)在區間(a,b)內有零點,故錯誤.
其中真命題的個數為1,
故選:C.


 核心素養學練評系列答案
核心素養學練評系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:高中數學 來源: 題型:
【題目】中國古代計時器的發明時間不晚于戰國時代(公元前476年~前222年),其中沙漏就是古代利用機械原理設計的一種計時裝置,它由兩個形狀完全相同的容器和一個狹窄的連接管道組成,開始時細沙全部在上部容器中,細沙通過連接管道流到下部容器,如圖,某沙漏由上、下兩個圓錐容器組成,圓錐的底面圓的直徑和高均為8 cm,細沙全部在上部時,其高度為圓錐高度的![]() (細管長度忽略不計).若細沙全部漏入下部后,恰好堆成一個蓋住沙漏底部的圓錐形沙堆,則此圓錐形沙堆的高為( )
(細管長度忽略不計).若細沙全部漏入下部后,恰好堆成一個蓋住沙漏底部的圓錐形沙堆,則此圓錐形沙堆的高為( )
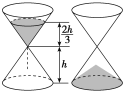
A.2 cmB.![]() cmC.
cmC.![]() cmD.
cmD.![]() cm
cm
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 、
、![]() 的定義域均為
的定義域均為![]() ,若對任意
,若對任意![]() ,且
,且![]() ,具有
,具有![]() ,則稱函數
,則稱函數![]() 為
為![]() 上的單調非減函數,給出以下命題:① 若
上的單調非減函數,給出以下命題:① 若![]() 關于點
關于點![]() 和直線
和直線![]() (
(![]() )對稱,則
)對稱,則![]() 為周期函數,且
為周期函數,且![]() 是
是![]() 的一個周期;② 若
的一個周期;② 若![]() 是周期函數,且關于直線
是周期函數,且關于直線![]() 對稱,則
對稱,則![]() 必關于無窮多條直線對稱;③ 若
必關于無窮多條直線對稱;③ 若![]() 是單調非減函數,且關于無窮多個點中心對稱,則
是單調非減函數,且關于無窮多個點中心對稱,則![]() 的圖象是一條直線;④ 若
的圖象是一條直線;④ 若![]() 是單調非減函數,且關于無窮多條平行于
是單調非減函數,且關于無窮多條平行于![]() 軸的直線對稱,則
軸的直線對稱,則![]() 是常值函數;以上命題中,所有真命題的序號是_________
是常值函數;以上命題中,所有真命題的序號是_________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左.右焦點分別為
的左.右焦點分別為![]() ,短軸兩個端點為
,短軸兩個端點為![]() ,且四邊形
,且四邊形![]() 的邊長為
的邊長為![]() 的正方形.
的正方形.
(Ⅰ)求橢圓的方程;
(Ⅱ)若![]() ,分別是橢圓長軸的左,右端點,動點
,分別是橢圓長軸的左,右端點,動點![]() 滿足
滿足![]() ,連結
,連結![]() ,交橢圓于點
,交橢圓于點![]() .證明:
.證明: ![]() 的定值;
的定值;
(Ⅲ)在(Ⅱ)的條件下,試問![]() 軸上是否存在異于點
軸上是否存在異于點![]() ,的定點
,的定點![]() ,使得以
,使得以![]() 為直徑的圓恒過直線
為直徑的圓恒過直線![]() ,
,![]() 的交點,若存在,求出點
的交點,若存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦距為
的焦距為![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點在橢圓
的對稱點在橢圓![]() 上.
上.
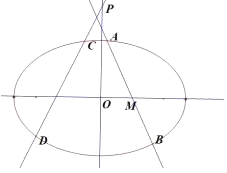
(1)求橢圓![]() 的方程;
的方程;
(2)如圖,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩個不同的點
交于兩個不同的點![]() (點
(點![]() 在點
在點![]() 的上方),試求
的上方),試求![]() 面積的最大值;
面積的最大值;
(3)若直線![]() 經過點
經過點![]() ,且與橢圓
,且與橢圓![]() 交于兩個不同的點
交于兩個不同的點![]() ,是否存在直線
,是否存在直線![]() (其中
(其中![]() ),使得
),使得![]() 到直線
到直線![]() 的距離
的距離![]() 滿足
滿足![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com